Расчет характеристик глиссирования плоско-килеватых корпусов

Одной из проблем, часто встречающихся в практике проектирования глиссирующих катеров, является определение оптимальной ширины b и угла глиссирования τ на тихой воде, обеспечивающих наименьшее сопротивление R и максимально достижимую скорость хода V при известной нагрузке Δ, продольной центровке x_g и угле килеватости β при заданной мощности N и определенном пропульсивном КПД движительного комплекса η.

В реальных условиях эксплуатации встречается несколько значений нагрузки и положений центра тяжести (ЦТ), поэтому оптимальная ширина глиссирования будет изменяться в широких пределах, вплоть до максимальной ширины днища по скуле. Определение этой величины необходимо еще в процессе разработки проекта катера, чтобы заранее рассчитать ширину установки продольных реданов, уступов или других брызгоотсекающих кромок, обеспечивающих отрыв потока от поверхности днища, не участвующей в создании гидродинамической силы поддержания.

Для прямого решения поставленной задачи использование известных расчетных методов затруднительно из-за необходимости выполнения ряда последовательных приближений, так как скорость и ширина глиссирования заранее неизвестны.¹

Форма смоченной поверхности современных остроскулых корпусов на режиме глиссирования, как известно, близка к призматической, т. е. имеет почти постоянную ширину и килеватость при наличии прямых линий батоксов. Угол килеватости обычно задается конструктивно, поскольку его выбор связан с определенным компромиссом, обусловленным стремлением получить более высокое гидродинамическое качество на тихой воде и одновременно обеспечить надлежащую мореходность с минимальными ударными перегрузками при движении на волнении. Кроме того, наличие килеватости благоприятно сказывается на управляемости и поворотливости катера.


Результаты испытаний, выполненных в опытовых бассейнах с плоско-килеватыми призматическими поверхностями, могут использоваться для гидродинамического расчета глиссирующих корпусов.

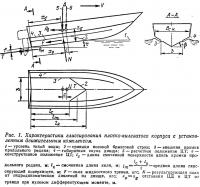
Рассмотрим систему сил, действующих на реальный глиссирующий корпус (рис. 1), приводимый в движение гребным винтом подвесного мотора или угловой колонки. При этом допустим, что векторы упора Т и гидродинамического сопротивления подводной части подвесного мотора соосны и параллельны килю, а линия действия аэродинамического сопротивления R_M проходит через ЦТ, который первоначально расположен над предполагаемым центром давления (ЦД).

Относительное сопротивление ε (или обратное качество) плоско-килеватой глиссирующей поверхности выражается известной формулой


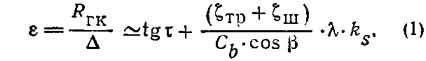
где R_ГК — сопротивление глиссирования голого корпуса (без выступающих частей), кгс;


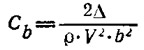
— коэффициент подъемной силы, в котором ρ = 102 кгс·с²/м⁴; К — скорость, м/с;

λ = l_m/b — относительное удлинение смоченной поверхности; k_s — коэффициент, учитывающий режим обтекания смоченной поверхности и влияние носовой брызговой струи.


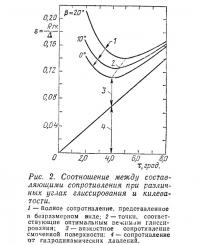
Первое слагаемое в (1) представляет сопротивление от гидродинамических давлений на днище, а второе — характеризует силу трения. На рис. 2 показано типичное соотношение между указанными составляющими в зависимости от угла глиссирования и килеватости днища.

Задача заключается в определении элементов глиссирования, соответствующих минимуму ε, имеющему место при всех углах килеватости.

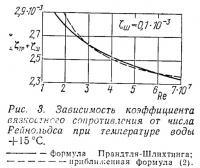
Суммарный коэффициент вязкостного сопротивления (ζ_ТР+ζ_Ш) в диапазоне чисел Рейнольдса


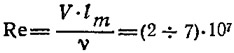
(рис. 3), охватывающем возможные скоростные режимы малых глиссирующих катеров, выразим следующей приближенной формулой:


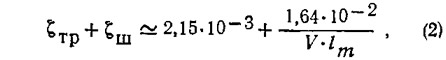
в которой принято: ζ_Ш=0,1·10^—3;
v = 1,141·10^—6 м²/с.

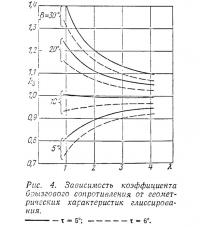
Множитель k_s в (1), графически представленный на рис. 4, при β≥10° достаточно надежно аппроксимируется формулой


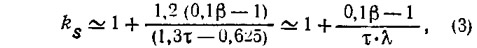
где β и τ выражены в градусах.


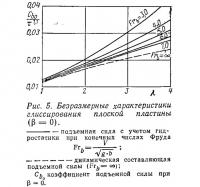
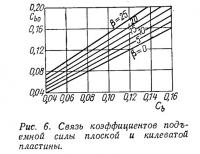
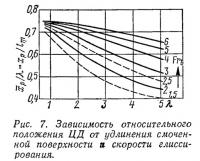
Для аналитического выражения А. входящего в (1) и (3), воспользуемся полуэмпирическими зависимостями (рис. 5, 6, 7), полученными А. Мюррэем (1950 г.) и Д. Савицким (1964 г.) и связывающими в безразмерном виде подъемную силу и положение ЦД плоско-килеватых глиссирующих пластин с их геометрическими и скоростными характеристиками.

После аппроксимации кривых на рис. 5, 6 и 7 в практическом диапазоне


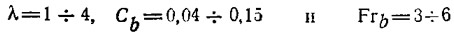
и выполнения аналитических преобразований (1) с учетом (2) и (3) находим оптимальный угол глиссирования


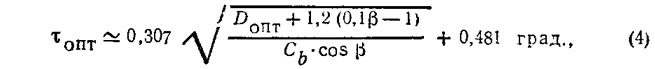
и далее — оптимальное удлинение смоченной поверхности


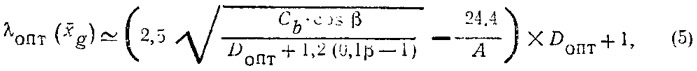
удлинение, зависящее от положения ЦД (рис. 7),



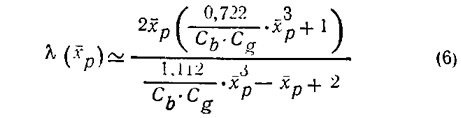
и, наконец, минимум относительного сопротивления



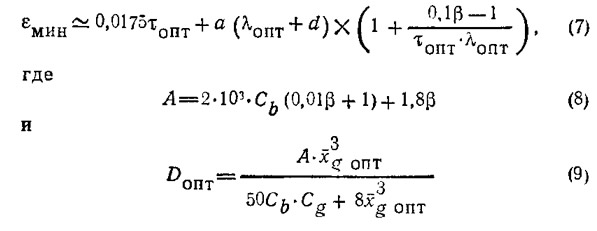
— вспомогательные параметры;


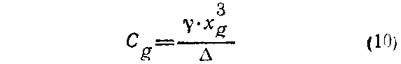
— безразмерный коэффициент продольной центровки (λ = 1000 кгс/м³);


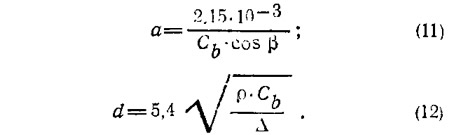
Оптимальное значение


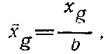
входящее во вспомогательный параметр (9), можно определить, полагая


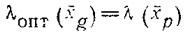
при х_р=x_g. Решение этого уравнения удобно выполнить графоаналитическим методом, задавая ряд значений С_b. С_g и х_g=x_p при постоянном β. Практический диапазон С_g укладывается в пределах C_g = 2÷8.


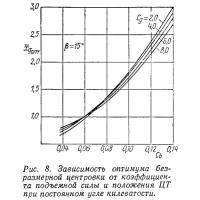
Для каждого угла килеватости можно затем построить график


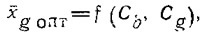
аналогичный представленному на рис. 8 для β=13°.
По результатам графоаналитической обработки серии указанных кривых, построенных в диапазоне β=10÷25°, получена простая ключевая формула для определения оптимума x_g, использование которой намного упрощает предыдущую расчетную процедуру:


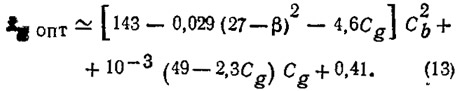
Зная проектные величины C_g и β и задаваясь рядом C_b, при помощи (13) легко найти x_{g опт} и затем D_опт в соответствии с (9), после чего можно перейти к определению оптимальных значений τ, λ и ε по формулам (4), (5) и (7).

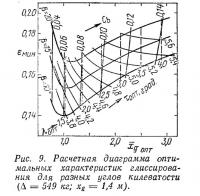
В качестве иллюстрации на рис. 9 приведена расчетная диаграмма оптимальных характеристик глиссирования в осях ε_мин—x_{g опт}, построенная для трех углов килеватости при водоизмещения Δ=549 кг и x_g=4 м. На кривых ε_мин нанесены линии постоянных значений τ_опт, λ_опт и С_b. Видно, что эта кривые имеют свой ярко выраженный минимум в области малых λ, практически недостижимых на практике из-за появления продольной неустойчивости глиссирования.

После расчета и построения кривой ε_мин для выбранного β на ней необходимо найти точку, соответствующую заданной мощности двигателя N (л. с.) и ожидаемому пропульсивному КПД η, учитывая при этом наличие сопротивления г — суммы сопротивления выступающих частей и аэродинамического сопротивления.

Поставленное условие можно выразить следующим образом:


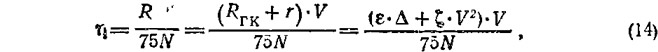
где R — полное сопротивление, кгс;
ζ = ζ_м + ζ_а — коэффициент суммарного сопротивления выступающих частей и воздушного потока.

Выражая V через в форме


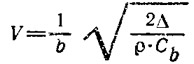
и учитывая, что b=x_g/x_g, можно привести (14) к требуемому виду:


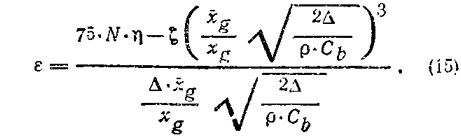
Если подставить в (15) сочетания C_b и x_{g опт}, соответствующие формуле (13) или рис. 9, то в итоге получим другую линию ε (x_g, C_b) точка пересечения которой с ранее построенной кривой ε_мин (рис. 10) даст искомые значения x_{g опт} и C_b. Знание этих величин позволит затем легко рассчитать остальные характеристики глиссирования. При оптимизации характеристик глиссирования должна рассматриваться гидродинамическая система в целом, то есть с учетом баланса сил и моментов, действующих на корпус при движении.

При распределении сил, показанном на рис. 1, неизбежно появление момента в продольной плоскости, вызывающего дополнительный дифферент ка корму, т. е. отклонение от оптимума τ. Действие этого момента необходимо компенсировать либо конструктивным наклоном оси вращения гребного винта относительно киля, либо смещением ЦТ в нос на величину с относительно расчетного положения ЦД:


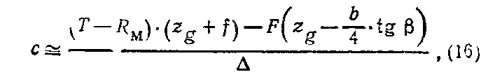
где f — заглубление оси гребного винта, z_g — возвышение ЦТ над килевой линией.

При использовании водометного движителя величина указанной поправки может оказаться намного меньше, так как линяя тяги проходит выше киля.

В рассматриваемом случае вертикальной составляющей упора можно пренебречь, допуская при этом cos τ ≈ 1. Корректировка положения ЦТ выполняется после определения составляющих R_M и F полного сопротивления R ≈ T. В связи с малой величиной этой поправки ее легко реализовать на практике за счет незначительного перераспределения составляющих нагрузки по длине.

Смоченную длину киля при глиссировании на расчетном режиме (рис. 1) можно определить по формуле


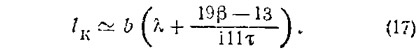
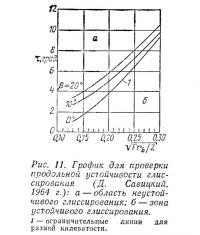
Наконец, важным моментом при уточнении продольной центровки катера является обеспечение продольной устойчивости движения на расчетном режиме. Такой контроль можно осуществить с помощью графика (на рис. 11) или же по формуле, сообщающей результаты модельных испытаний при β=0÷21°;


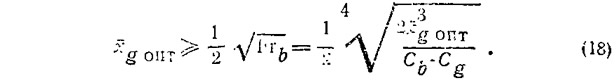
При расчете по формуле (15) может возникнуть вопрос, какие величины η и ζ следует принимать? В случае использования подвесного мотора или угловой колонки с оптимально спроектированным гребным винтом можно принять η= 0,55÷0,6 в зависимости от качества обработки лопастей винта и подводной части мотора. Для водометного движителя эффективный КПД будет несколько ниже и обычно составляет η=0,45÷0,5 в зависимости от правильности подбора элементов водопроточной части и рабочего колеса, однако снижение КПД в этом случае компенсируется отсутствием выступающих частей, которые, как отмечено выше, могут составлять значительную долю полного сопротивления.

По данным гидродинамических испытаний подвесных моторов, коэффициенты сопротивления их подводной части имеют следующие значения: ζ_М=0,135 для моторов «Вихрь-25» и «-30» и ζ_М=0,175 для моторов «Нептуи-23».

Коэффициент аэродинамического сопротивления выражается в зависимости от площади лобового сечения корпуса и может оцениваться величиной ζ_а=0,035 S_лоб, где S_лоб в м².

Расчет элементов глиссирования выполняется в следующем порядке:

1. В результате проработки общего расположения задаются Δ, β, x_g, N, η и вычисляется С_g в соответствии с (10), а также устанавливается ряд возрастающих значений C_b=0,04÷0,4, например, с интервалом 0,02.

2. Рассчитывается x_{g опт} по формуле (13) последовательно для всех C_b при постоянном β.

3. Определяются А и D_опт по формулам (8) и (9) для каждого из полученных в п. 2 сочетаний C_b и x_{g опт}.

4. Рассчитываются τ_опт и затем λ_опт по формулам (4) и (5).

5. После вычисления a и d по формулам (11) и (12) с учетом результатов п. 4 рассчитываем кривую ε_мин при каждом x_{g опт} и C_b.

6. Строим график оптимальных значении ε, λ, τ и C_b в функции от x_g по аналогии с рис. 10.

7. Производим вычисление ε по формуле (15), подставляя в нее сочетания x_{g опт} и C_b, найденные в п. 2. Точка пересечения полученной линии ε=f(x_g) с ранее построенной кривой ε_мин (п. 6 — рис. 10) дает расчетные оптимальные значения ε, C_b, x_g, τ и λ.

8. Далее определяем остальные характеристики глиссирования:


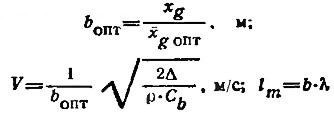
и l_к по формуле (17).

9. Зная ε, Δ, ζ и V, рассчитываем полное сопротивление глиссирования R=εΔ+ζV², равное необходимому упору Т гребного винта, и проверяем замкнутость решения на основе равенства (14).

10. Находим сопротивление трения F=R—0,0175τ·Δ—ζ·V² и производим корректировку положения ЦТ по формуле (16).

11. Выполняем контроль продольной устойчивости глиссирования по графику (рис. 11) или формуле (18).

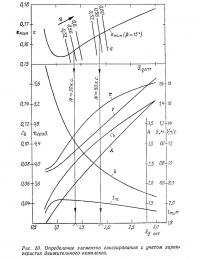
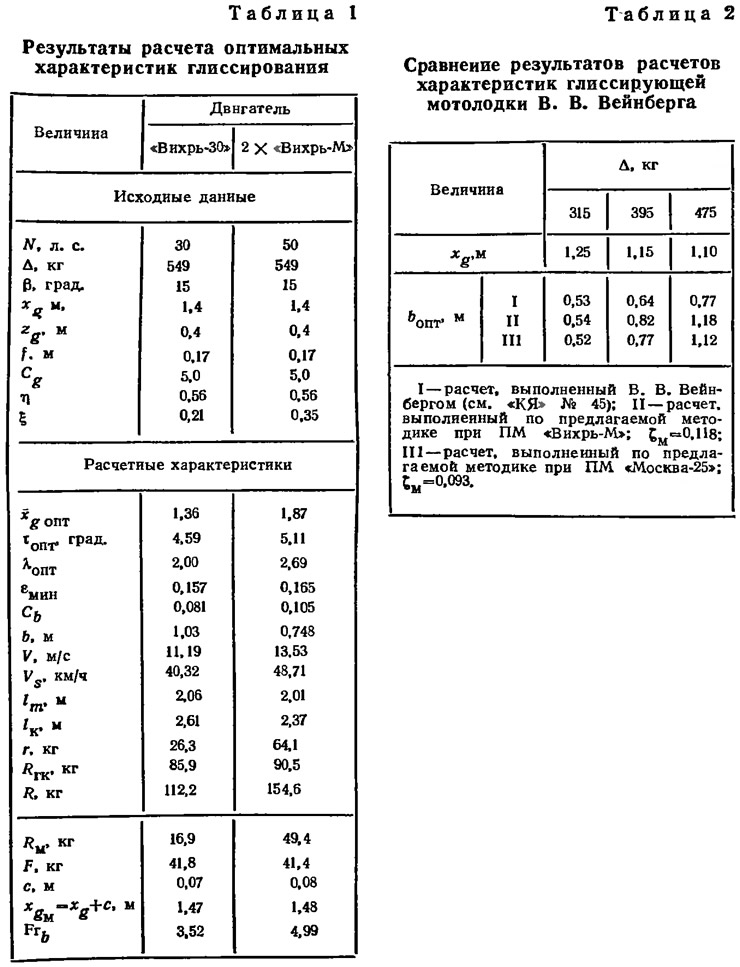
В качестве примера на рис. 10 и в табл. 1 представлены результаты расчета оптимальных характеристик глиссирования для катера весом 549 кг при β=15° и x_g=1,4 м. Рассмотрены два варианта энерговооруженности: с одним мотором «Вихрь-30» и с двумя моторами «Внхрь-М» при η=0,56.

Сравнение полученных расчетных данных показывает, что при двухмоторном варианте увеличение мощности почти на 67% приводит к повышению скорости всего на 21%. Доля сопротивления выступающих частей в этом случае значительно возрастает и составляет более половины сопротивления голого корпуса и почти одну треть полного ходового сопротивления. Следовательно, с точки зрения расхода топлива выигрыш в скорости за счет повышения энерговооруженности не всегда оправдан и требует специального обоснования с учетом характеристик движительного комплекса и величины передаваемой мощности.

Представляет интерес, насколько элементы глиссирования, рассчитанные предлагаемым методом, будут отличаться от характеристик натурных проектов, ранее опубликованных в журнале. С этой целью был выполнен сравнительный расчет для трек вариантов нагрузки и центровки на примере мотолодки, спроектированной и испытанной В. В. Вейнбергом (см. «КЯ» №44). Для оценки влияния формы выступающих частей моторов на величину скорости рассмотрены варианты с подвесными моторами «Вихрь-М» и «Москва-25», имеющими одинаковую мощность N=25 л. с., но отличающимися сопротивлением подводных частей (см. рис. 20 в №44). Исходные да иные и результаты расчета при η=0,6 приведены в табл. 2 и на рис. 12. Видно, что расчетная скорость мотолодки (β=21°) с мотором «Москва-25», определенная предлагаемым способом, близка к скорости натурного образца. При установке мотора «Вихрь-М» скорость хода несколько снижается из-за увеличения сопротивления подводной части мотора при той же мощности.

Однако ширина глиссирования, указанная В. В. Вейнбергом, меньше ширины, рассчитанной предлагаемым методом. Это отличие можно частично объяснить несколько завышенной скоростью в расчете В. В. Вейнберга, где не учтено воздушное сопротивление корпуса и влияние масштаба на гидродинамическое качество глиссирования.

Расчеты по предлагаемой методике позволяют решать и ряд задач при эксплуатации лодки. Так, расчет оптимальных характеристик глиссирования, выполненный для серийной мотолодки «Днепр» (Δ=660 кг; β=14°) с ПМ «Вихрь-30», позволил проанализировать роль центровки и повышения КПД движительного комплекса. Изменение х_g с 1,4 до 1,6 при η=0,58 дает изменение скорости с 38,5 до 38,9 км/ч при уменьшении R=Т со 121,9 до 120,7 кгс. Повышение η до 0,60 сразу же повышает скорость на 1 км/ч при некотором возрастании R=Т со 121,9 до 122,6 кгс при x_g=1,4 и т. д. Расчетная ширина глиссирования во всех случаях получалась меньше, чем конструктивная ширина днища «Днепра» по скуле. Имеющийся запас ширины позволяет несколько увеличивать нагрузку без значительного падения скорости.

Примечания

1. См. также статью В. В. Вейнберга «Глубокое V: за и против» в «КЯ» №44, в которой подробно описывается физика явлений.