Расчет гребного винта с помощью микрокалькулятора

Выбор оптимального гребного винта — желанная цель любого водномоторника. Однако на практике приходится сталкиваться с большими трудностями, связанными с громоздкими расчетами и различными ограничениями, например — связанными с изготовлением винтов в домашних условиях Все же главной трудностью для многих любителей является именно большой объем вычислений, необходимых для выбора оптимального варианта из нескольких возможных.

Эту трудоемкую работу существенно может упростить использование микрокалькуляторов.

В принципе все многообразие проблем, с которыми приходится сталкиваться, проектируя двигательно-движительный комплекс, можно свести к следующим основным вариантам.

1. Расчет оптимального гребного винта, который обеспечивает катеру требуемую скорость. В этом случае заданными считаются: скорость v катера, его сопротивление при этой скорости — R; характеристики взаимодействия винта и корпуса — коэффициент попутного потока w, засасывания t и влияния неравномерности поля скоростей i; диаметр гребного винта D. Искомые величины — мощность N и частота вращения n двигателя, геометрические элементы гребного винта — его дисковое θ и шаговое Н/D отношения.

2. Расчет оптимального гребного винта, обеспечивающего катеру максимальную скорость движения. Заданы: зависимость сопротивления катера от скорости R(v); w, t, i: N, n. Ищутся: максимальная скорость v_max, геометрические элементы гребного винта — D, θ, H/D.

3. Расчёт неоптимального гребного винта, обеспечивающего полное использование мощности двигателя. Заданы: R(v); w, t, i; N, n; D. Находятся: v; θ; H/D.

4. Определение скорости катера и режима работы двигателя с гребным винтом, характеристики которого известны. Заданы: R(v), w, t, i; N, n; D, θ, H/D. Искомые величины: v; N' и n' — мощность и частота вращения, развиваемые двигателем (N'≤N и n'≤n, при условии, что N и n соответствуют номинальному режиму работы рассматриваемого двигателя).

Перечисленные выше задачи достаточно эффективно решаются при наличии диаграмм для расчета гребных винтов.¹ Однако, наряду с очевидными преимуществами представление гидродинамических характеристик (ГДХ) гребных винтов в виде диаграмм имеет и ряд недостатков: существенно затрудняется применение вычислительной техники в расчетах; для промежуточных значений шагового и дискового отношений приходится прибегать к интерполяции; доступные диаграммы имеют малый масштаб, что приводит к появлению погрешностей в расчетах.


Перечисленные недостатки могут быть устранены при аналитическом представлении ГДХ гребных винтов серии. Известны аппроксимации кривых действия гребных винтов полиномами, однако в таком виде они могут использоваться только при расчетах на ЭВМ.² Для ручного счета, в том числе и с помощью программируемых микрокалькуляторов, подобное полиномиальное представление ГДХ гребных винтов совершенно неприемлемо.

Обработка результатов испытаний трехлопастных гребных винтов показала, что их ГДХ могут быть представлены в аналитическом виде в форме, одинаково удобной как для ручного, так и для автоматизированного счета. Исходным материалом служили корпусные и машинные диаграммы широколопастных гребных винтов с сегментным сечением профиля. Эти диаграммы были получены Г. Звездкинон для трех серий винтов, каждая из которых имела фиксированное дисковое отношение — 0,5; 0,8; 1,1. Шаговое отношение, в сериях составляло — 0,6; 0,8; 1,0; 1,2; 1,4; 1,6.

В результате обработки этих экспериментальных данных Ф. Соколовым и А. Якушенко были получены следующие зависимости:


Показатели степеней в (1) и (2) являются функциями дискового отношения:


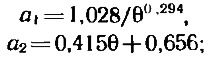
коэффициенты в (2)÷(5) определяются зависимостями:



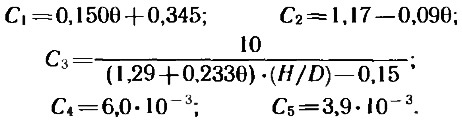
При проектировании оптимальных гребных винтов используются коэффициенты задания, определяемые, как известно, выражениями:


где N_p — мощность, подводимая к гребному винту, л. с.

Линии оптимальных значений указанных коэффициентов на диаграммах для рассматриваемых серий хорошо аппроксимируются линейными зависимостями:


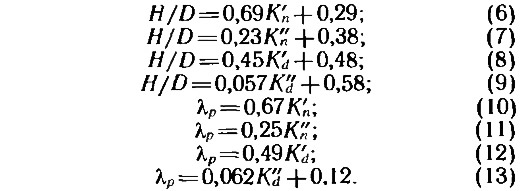
Выражения (1)÷(13) в аналитическом виде представляют все данные диаграмм для расчета широколопастных гребных винтов, а следователь но, могут использоваться для проектирования движительно двигательного комплекса катера.

Геометрия гребного винта во многом определяется дисковым отношением, которое в свою очередь выбирается из условия обеспечения прочности и отсутствия вредных последствий кавитации. Для рассматриваемых широколопастных гребных винтов с использованием методики В. М. Лаврентьева было получено выражение для минимально допустимого, с точки зрения прочности, дискового отношения:



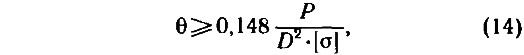
где Р — упор гребного винта, кгс;
D — диаметр винта, м;
[σ] — допускаемые напряжения, кгс/см².

Можно рекомендовать для стальных, латунных и бронзовых винтов принимать [σ]=550, а для силуминовых — 350 кгс/см².

Проверка на кавитацию производится в окончательной стадии расчета, когда известны шаговое отношение гребного винта и режим его работы, т. е. относительная поступь. Построенный Г. Звездкиной график позволяет определить критическое значение относительной поступи в зависимости от шагового и дискового отношений, а также от числа кавитации. Выполнение условия λ_р>λ_{р кр} обеспечивает отсутствие второй стадии кавитации. Аппроксимация указанных графиков позволила предложить следующую зависимость:


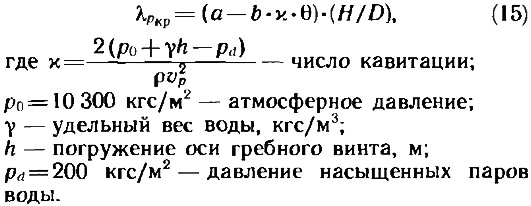
Коэффициенты а и b в выражении (15) зависят от величины шагового отношения и могут приниматься в соответствии с данными табл. 1.

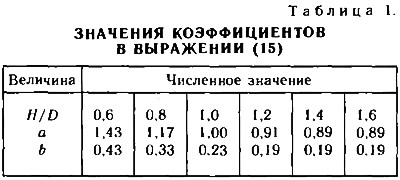
Формула (15) справедлива только в том случае, когда произведение х·θ изменяется в пределах 0,7≤х·θ≤1,0, однако этого диапазона хватает для проверки тех винтов, работа которых может сопровождаться кавитацией. Величины коэффициентов а и b для промежуточных значений шагового отношения можно определять линейной интерполяцией. В расчетном режиме движения кавитации практически не стоит опасаться, если x≥1,5.


В условиях существенной неравномерности поля скоростей, в частности для значительных скосов потока, когда угол наклона гребного вала больше 10°, возрастает опасность кавитационной эрозии винта. В подобной ситуации рекомендуется увеличивать дисковое отношение, определенное с помощью выражения (15), на 20%, однако не более чем до θ=1,2, так как дальнейшее его увеличение практически не приводит к отдалению кавитации. Если произведенная проверка покажет, что найденное по (14) значение 0 не обеспечивает отсутствия кавитации, дисковое отношение следует увеличить и заново произвести расчет винта.

Гребные винты рассматриваемой серии имеют постоянный вдоль радиуса шаг; относительный диаметр ступицы составляет


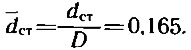
Контур спрямленной поверхности лопасти имеет симметричную форму, а его ординаты однозначно определяются величиной дискового отношения:


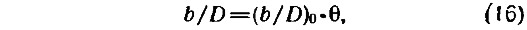
где b — ширина (хорда) профиля лопасти на данном радиусе, м;
(b/D)₀ — относительная ширина лопасти для θ=1,0 (табл. 2).

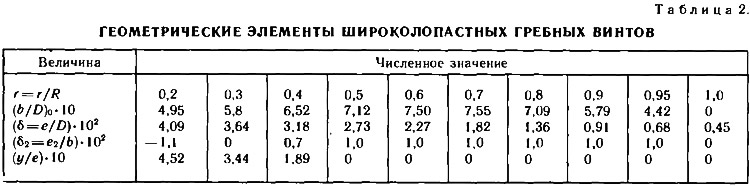
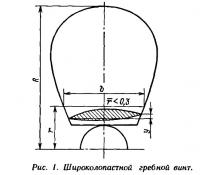
Профиль сечения лопасти имеет сегментную форму; на относительных радиусах r=r/R<0,3 сегмент двояковыпуклый с приподнятой входящей кромкой; на больших радиусах — выпукло-вогнутый. Максимальные толщина и стрелка погиби профиля расположены посередине хорды и так же, как и подъем входящей кромки, являются функциями относительного радиуса. На рис. 1 схематически изображен гребной винт, а в табл. 2 приводятся значения всех необходимых для построения его чертежа относительных величин.

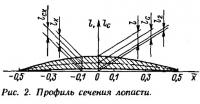
Профиль сечения лопасти (рис. 2) представляет собой параболический сегмент. Для его построения сначала проводим среднюю линию, а затем откладываем от нее в обе стороны половину толщины профиля, найденной для данного отстояния точки от середины хорды.


Ординаты средней линии и толщина профиля рассчитываются по аналогичным формулам:


Используя приведенные рекомендации и ориентируясь на рис. 1 и 2, можно выполнить чертеж гребного винта. Следует подчеркнуть, что приведенные выше материалы по гидродинамическим и геометрическим характеристикам гребных винтов в полной мере относятся только к винтам Г. Звездкиной. Штатные гребные винты отечественных подвесных моторов имеют иную геометрию; больший относительный диаметр ступицы и меньшую стрелку погиби. Однако проведенное автором сопоставление ГДХ двух штатных гребных винтов с рассчитанными по формулам (1)÷(5) показывает, что в рабочем диапазоне относительной поступи λ_р= 0,5÷0,9 можно пользоваться следующими зависимостями:


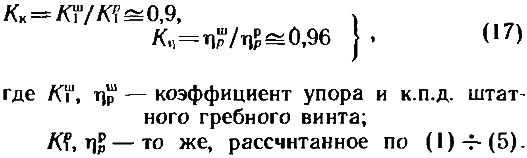
Сравнение производилось для винтов подвесных моторов «Вихрь» (D=0,24 м; H=0,30 м; d_ст=0,063 м; θ=0,527) и «Нептун-23» (D=0,23 м; H=0,28 м). В обоих случаях брались данные для полированных гребных винтов. Для окрашенных винтов можно рекомендовать снижать коэффициент упора и к.п.д. приблизительно на 5% по сравнению с полированными. Все рекомендации, относящиеся к штатным винтам, получены на основании обработки ограниченного числа данных, поэтому они могут служить только для самых предварительных оценок.

В ряде случаев, в частности при изготовлении гребного винта к подвесному двигателю, может оказаться полезной откидка лопасти в корму. Если угол откидки лопасти не превышает 10—15°, то это практически не оказывает влияния на ГДХ винта.

И еще один момент, который необходимо отметить. Винты Г. Звездкиной имеют относительно небольшой диаметр ступицы (d_ст=0,165 D), чего не всегда удается достичь, изготавливая винт для катера. Учесть влияние увеличения d_ст можно, пользуясь следующими рекомендациями: при


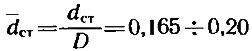
никаких поправок вводить не надо; при увеличении относительного диаметра ступицы до d_ст=0,3 к.п.д. винта уменьшится на 2—3%; в диапазоне d_ст=0,2÷0,3 для оценки падения к.п.д. можно применять линейную интерполяцию.

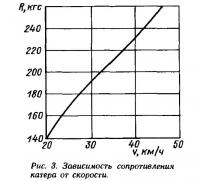
Изложенное выше проиллюстрируем несколькими примерами. Предположим, нам нужно спроектировать гребной винт к катеру типа «Суперкосатка» водоизмещением 1000 кг, зависимость сопротивления которого от скорости известна (рис. 3). Прежде всего нужно выбрать необходимый двигатель, позволяющий достичь требуемой скорости, скажем 36 км/ч. Ориентируясь на установку двух отечественных подвесных моторов («Нептун», «Вихрь», «Москва») и зная их габариты, задаемся величиной диаметра гребного винта θ=0,23 м.

Наиболее подходящей для данного случая методикой расчета элементов оптимального гребного винта будет схема 1, в которой используется коэффициент задания K'_d.

Схема 1. Заданы: скорость движения v=36 км/ч; сопротивление катера с учетом выступающих частей (рис. 3) R=214 кгс; коэффициенты взаимодействия винта и корпуса w=0,025, t=0,045; i=1,0.

Кроме того известны: ρ=102 кг·с²/м⁴, [σ]=550 кгс/см².

Расчет производим в такой последовательности:

— находим необходимый упор одного винта P=P_e/(1—t)=R/2(1—t)=112 кгс;

— определяем среднюю скорость в диске винта v_р=v(1—w)=9,75 м/с;

— рассчитываем:

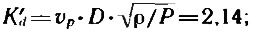
— используя (8), (12), (14), находим H/D=1,44; λ_p=1,05; θ=0,570; n=v_p/λ_pD = 40,4 об/с; K₁=0,240;

— зная H/D и θ, с помощью (5) и (4) определяем коэффициенты К₂₀=0,0125 и K₂=0,0580; к.п.д. гребного винта


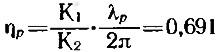
и требуемую мощность двигателя:


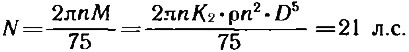
Ту же величину можно рассчитать и таким образом:


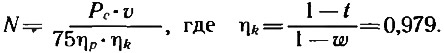
На основании приведенного выше расчета заключаем, что для обеспечения катеру требуемой скорости необходимы два двигателя мощностью по 21 л. с. с частотой вращения на валу винта 40,4 об/с. Поскольку подвесных моторов, в точности отвечающим данным требованиям, не существует, останавливаемся на «Нептуне-23», мощность которого 23 л. с. при частоте вращения 5000 об/мин, что с учетом передаточного числа редуктора на валу винта составляет 48,1 об/с. В силу того, что рассчитанные значения мощности и оборотов не совпадают с таковыми у выбранного двигателя, следует произвести новый расчет винта, который с данным подвесным мотором обеспечивал бы катеру максимальную скорость движения.

Схема 2. Заданы: зависимость сопротивления катера от скорости R(v) — рис. 3; номинальные характеристики двигателя N=23 л. с.; n'=5000 об/мин (n=48,1 об/с); максимально допустимый диаметр гребного винта D_max=0,23 м.

Коэффициенты взаимодействия, допускаемые напряжения и плотность пресной воды здесь и в дальнейшем принимаются такими же, как и в предыдущем примере.

Выбор оптимального гребного винта, отвечающего настоящему заданию, можно производить двумя способами: с помощью коэффициентов задания К'_n или К"_n.

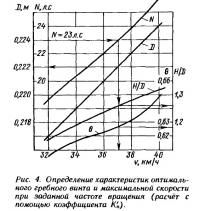
Рассмотрим сначала первый из них. Расчеты будем производить для ряда скоростей в районе ожидаемой. Хотя мощность выбранного двигателя и превышает рассчитанную, в принципе мы можем и не достичь требуемой скорости 36 км/ч, поскольку частота вращения винта существенно отличается от найденной выше. Поэтому будем рассматривать такой диапазон скоростей, чтобы ожидаемая находилась внутри него. Дальнейшие расчеты удобно вести в табличной форме (табл. 3).

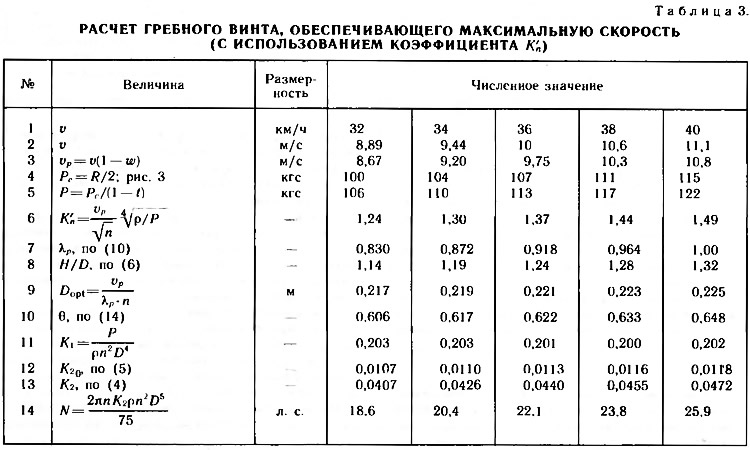
В последней строке таблицы мы получаем мощность, необходимую для обеспечения требуемой скорости при заданной частоте вращения гребного винта. По результатам расчета строим зависимости H/D, D_opt, θ, N в функции от скорости — рис. 4. В точке, где потребная мощность равна номинальной мощности выбранного двигателя N = 23 л. с., находим: H/D = 1,26; D_opt = 0,222 м; θ = 0,626; v = 37,1 км/ч.

Подсчитав к.п.д. винта

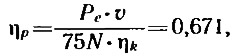
убеждаемся, что его эффективность ниже, чем была в схеме 1. Это объясняется увеличением частоты вращения и, как следствие, снижением величины оптимального диаметра. Принимая погружение оси гребного винта равным h = 0,2 м, найдем: х = 2,0. Поскольку х>1,5, проверять винт на кавитацию нет необходимости.

Схема 3. Ту же задачу, что и в предыдущем примере, будем решать с помощью коэффициента задания К"_n.

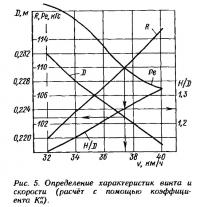
Расчеты приведены в табл. 4, по результатам которой построен график — рис. 5.

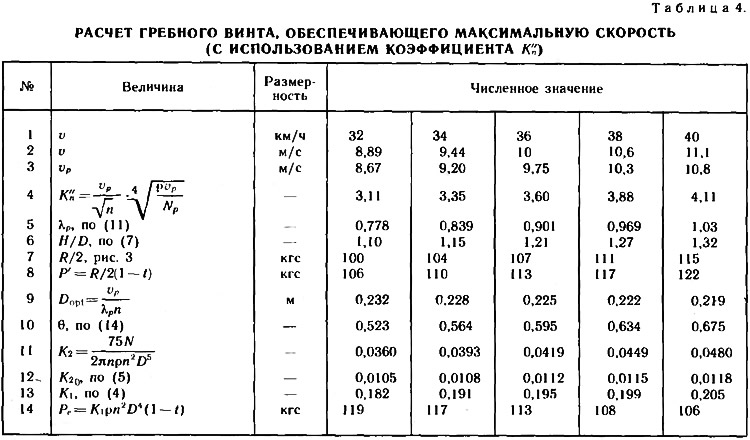
Строка 8 табл. 4 нужна только для того, чтобы рассчитать необходимое значение дискового отношения θ. Сравнение сопротивления (строка 7) и создаваемой гребным винтом полезной тяги (строка 14) позволяет определить как максимальную скорость, так и характеристики винта (рис. 5): v = 37,4 км/ч; H/D = 1,25; D_opt = 0,223 м. Незначительные различия в результатах расчетов по схемам 2 и 3 объясняются неизбежными погрешностями как аппроксимаций - выражения (1)÷(13), так и расчетов и графических построений.

В рассмотренном выше примере (схемы 2 и 3) для всех скоростей мы имели D_optmax=0,23 м. Однако возможен и другой вариант, когда диаметр оптимального винта окажется больше, чем максимально допустимый. В таком случае, очевидно, должно быть принято D=D_max. Соответственно изменятся и последовательность расчета, и его результаты.

Проиллюстрируем это на примере табл. 3, взяв последний столбец (v = 40 км/ч) и приняв, что максимальный диаметр составляет D_max = 0,21 м.

Схема 4. До девятой строки расчет (табл. 3) остается неизменным. Однако, поскольку D_opt>D_max, принимаем D = D_max = 0,21 м. При этом найденные в строках 7 и 8 и соответствующие оптимальному винту значения λ_р и Н/D уже не будут отвечать винту с D = 0,21 м. Таким образом определению подлежат величины: θ, λ_р, К₁, N и Н/D. Для рассматриваемого примера (v = 40 км/ч; Р_e = 115 кгс; D = 0,21 м) находим: θ = 0,744; K₁ = 0,266; λ_р = 1,07.

Наибольшие сложности возникают с определением шагового отношения. Для этого необходимо решить уравнение (1) относительно H/D, входящего в него в неявном виде. Используя выражения (2) и (3), преобразуем (1) к виду:

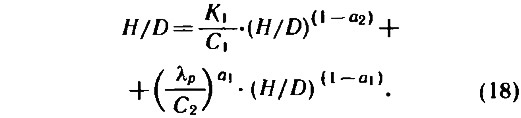
где выражения для показателей степеней а₁ и а₂ и коэффициентов С₁ и С₂ мы имели выше. Рассчитываем:

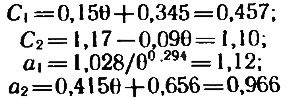
и окончательно получаем:

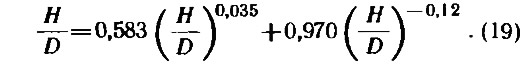
Решить это уравнение можно либо графически, задаваясь величиной шагового отношения в пределах 0,6÷1,6, либо методом последовательных приближений. Используем последний путь, приняв в качестве нулевого приближения

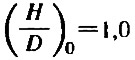
и вводя требование, чтобы погрешность вычислений не превышала

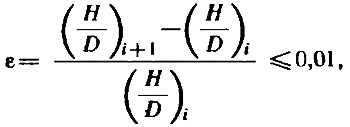
где i — номер приближения.

Последовательность решения:

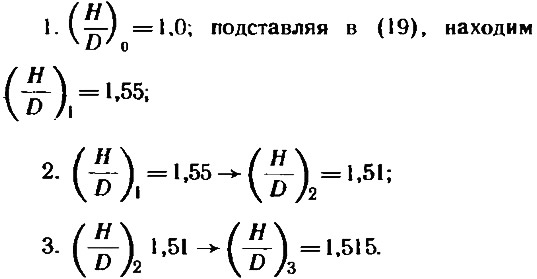
Уже второе приближение дает искомый результат с требуемой точностью: H/D = 1,51 Далее, используя (5) и (4), находим: К₂₀ = 0,013; К₂ = 0,0678; η_p = 0,668; N = 26,1 л. с.

Схема 5. Большой интерес представляет оценка ходовых качеств катера с подвесным мотором и штатным гребным винтом. В этом случае заданными являются: зависимость сопротивления катера от скорости; внешняя характеристика двигателя — зависимость его мощности от частоты вращения при полностью открытой дроссельной заслонке; геометрические характеристики гребного винта. Определяются максимальная скорость и режим работы двигателя, который в общем случае будет отличаться от номинального.

В качестве примера рассмотрим все тот же катер типа «Суперкосатка» и найдем его скорость под одним двигателем «Вихрь-30» со штатным гребным винтом.

Итак, задано: R(v) — рис. 3; внешняя характеристика двигателя — кривая N_дв = f(n) на рис. 7; геометрия гребного винта — D = 0,24 м; Н = 0,30 м; θ = 0,527. Передаточное число редуктора равно 14:24, винт считаем полированным.

Необходимые расчеты производим в следующем порядке:

— используя (2), (3) и (5), для заданных значений Н/D и θ определяем K_1max= 0,515; λ_pmax= 1,40; K₂₀= 0,0114;

— задаваясь рядом значений относительной поступи λ_р, по (1) и (4) находим расчетные величины коэффициента упора К^p₁ и момента К^p₂ винта, а затем и его к.п.д.;

— вводим поправки (17), учитывающие отличия штатного винта от винтов рассматриваемой серии.

Основные результаты такого расчета для трех значений поступи сведены в табл. 5.

Информация об изображении
Рис. 6. Гидродинамические характеристики штатного гребного винта

 

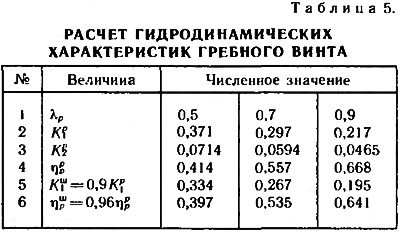
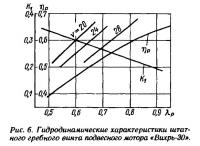
По данным табл. 5 строим кривые действия |K₁(λ_p) и η_p(λ_p)| штатного гребного винта — рис. 6. Далее, задавшись тремя значениями скорости и рядом частот вращения двигателя, подсчитаем соответствующие относительные поступи и необходимые коэффициенты упора — табл. 6.

В строке 2 таблицы приведена частота вращения гребного винта с учетом передаточного числа редуктора.

Нанеся полученные зависимости K₁(λ_p) на рис. 6, в точках их пересечения с кривой K₁(λ_p), соответствующей рассматриваемому гребному винту, найдем для каждой скорости единственно возможный режим работы гребного винта — сочетание K₁, λ_p и η_p. Для найденных режимов рассчитаем требуемые значения частоты вращения и мощности двигателя — табл. 7.

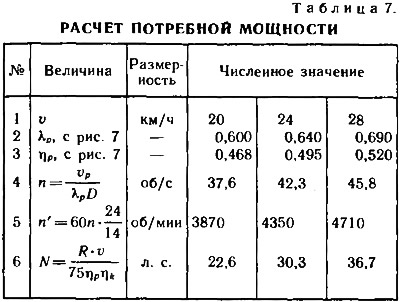
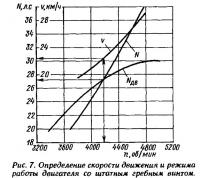
Нанося результаты расчета на график (рис. 7), находим точку пересечения кривой потребной мощности с располагаемой мощностью — внешней характеристикой двигателя «Вихрь-30». Эта точка и определяет искомые максимальную скорость v≈22,4 км/ч и режим работы двигателя: N≈27,2 л. с., п'≈4180 об/мин.

Информация об изображении
Рис. 7. Определение скорости движения и режима работы двигателя

 

Из расчета следует, что гребной винт в данном случае является гидродинамически тяжелым, т. е. его шаг слишком велик. Более того, винт не оптимален: его к.п.д. составляет всего η_p = 0,472, т. е. используемая винтом мощность перерабатывается с весьма низкой эффективностью (в предыдущих расчетах η_p = 0,65÷0,69).

Задачи, подобные последней, могут возникать и в том случае, если для расчетного режима выбран оптимальный гребной винт. Изменение загрузки катера (его водоизмещения либо центровки), движение в условиях волнения — все это приводит к изменению сопротивления, т. е. к изменению режима работы двигателя и гребного винта. Нарушается соответствие винта двигателю, т. е. условие использования номинальной мощности при номинальной частоте вращения. Винт становится либо гидродинамически легким, когда сопротивление уменьшается по сравнению с расчетным, либо тяжелым. В обоих случаях винт не использует номинальной мощности двигателя. Для исследования этих режимов да и любых других, которые могут встретиться на практике, удобнее всего пользоваться паспортной диаграммой. Пос роение последней может оказаться необходимым при проектировании гребного винта для быстроходных судов с явно выраженным горбом сопротивления (например, для катеров на подводных крыльях). В этом случае возможен вариант, когда винт, обеспечивая расчетный режим движения с высокой скоростью, не сможет преодолеть горба сопротивления. Приведенные выше аналитические выражения для ГДХ широколопастиых гребных винтов могут использоваться и для построения паспортной диаграммы.

Все приведенные выше расчеты могут эффективно выполняться с помощью программируемых микрокалькуляторов (например, «Электроника БЗ-34»). Это особенно удобно при проведении повторяющихся расчетов с вариацией как элементов задания, так и их типов.

В заключение хотелось бы отметить, что все рассмотренные выше примеры в определенной степени условны — их цель проиллюстрировать методику решения различных типов задач, связанных с выбором гребного винта.

Примечания

1. Выбор гребного винта в идеале сводится к определению таких его элементов, чтобы в расчетном режиме этот ГВ был оптимальным, т. е. имел наибольший возможный к.п.д. На практике приходится порой сталкиваться с такими ограничениями, которые делают оптимизацию винта невозможной; приходится выбирать такой ГВ, который выполнял бы условия задания при всех существующих ограничениях наилучшим образом.

2. Русецкий А. А., Жученко М. М., Дубровин О. В., Судовые движители, «Судостроение», Д., 1971; Хейфец Л. Л., Гребные винты для катеров, «Судостроение», Л., 1980.