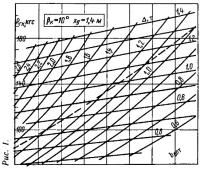
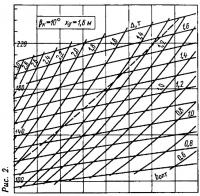
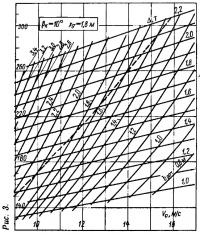
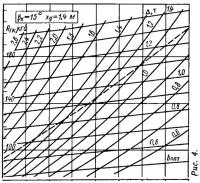
Результаты указанных расчетов оказалось возможным свести в одну корпусную диаграмму, связывающую весовую нагрузку Δ и оптимальную ширину глиссирования b со скоростью хода V и сопротивлением Rгк при заданном угле килеватости βк и продольной центровке xg. Пример использования такой диаграммы содержится в статье «Как рассчитать оптимальный водомет» — см. «КиЯ» №119 за 1986 г., рис. 13.
В дальнейшем несколько аппроксимирующих формул, входящих в методику, были уточнены, а последовательность самого расчета приведена к форме, упрощающей построение диаграммы.
Как отмечено выше, каждая корпусная диаграмма рассчитывается для фиксированных значений βк (град.) и xg (м) Вариация
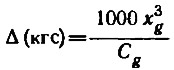
производится через равные числовые промежутки в пределах выполнения неравенства 2≤Cg≤6, лимитирующего область применения уточненных формул.
Ширина глиссирования b (м) задается в ожидаемом практическом диапазоне с постоянным интервалом (например, через 0,1 м).
Расчет корпусной диаграммы выполняется в следующем порядке.
1. Вычисляются вспомогательные коэффициенты оптимальной продольной центровки (при заданном Cg):
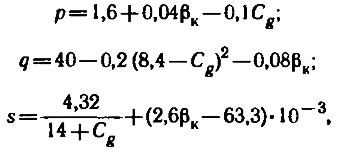
с использованием которых для заданного ряда ожидаемых bопт далее рассчитывается оптимальный коэффициент подъемной силы:
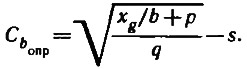
2. Определяются число Фруда по ширине глиссирования Frb, расчетная скорость V (м/с) и вспомогательные коэффициенты А, а и d:
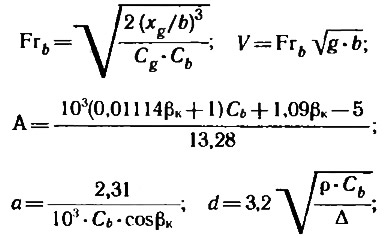
где ρ=102 кгс·с2/м4.
3. Рассчитываются оптимальное удлинение глиссирующей поверхности и соответствующий ему угол атаки:
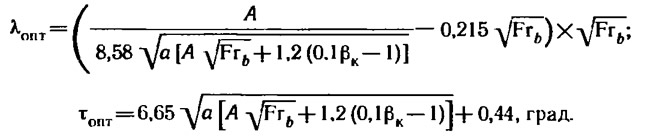
4. После этого вычисляется минимальное значение обратного качества и определяется сопротивление голого корпуса:
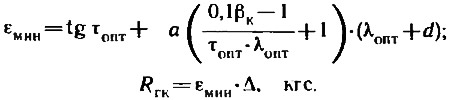
5. По заданному ряду bопт строятся линии постоянных Δ в координатах Rгк—V, а точки с одинаковыми значениями bопт на каждой из этих линий соединяются плавными кривыми, образующими линии постоянных bопт.
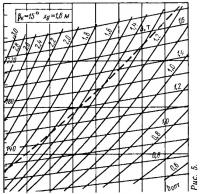
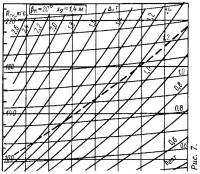
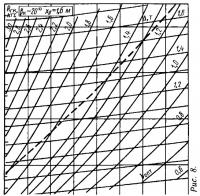
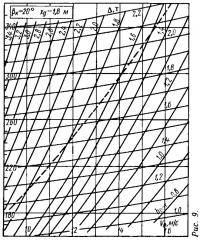
Для возможности оперативной оценки ходкости малых глиссирующих катеров с плоско-килеватыми обводами были рассчитаны и построены корпусные диаграммы для трех значений βк (10; 15 и 20°) и трех величин продольной центровки xg (1,4; 1,6; 1,8 м), охватывающих диапазон водоизмещений Δ=500÷2200 кг (рис. 1—9).
На каждой диаграмме пунктиром нанесена линия bкрит, определяющая вероятность появления продольной неустойчивости глиссирования (в области диаграммы выше этой линии — при bопт>bкрит).
Критическую ширину глиссирования в каждом случае можно приближенно оценить по формуле:
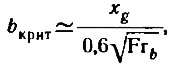
полученной на основе модельных испытании серии плоско-килеватых корпусов в опытовом бассейне.
В случае задания промежуточных значений Δ, βк, xg и V сопротивление и ширину глиссирования можно легко найти путем интерполяции. Например, требуется определить Rгк и bопт для Δ=1100 кг, βк=17,5° и xg=1,5 м при V=45 км/ч.
Еля этого используются четыре диаграммы — для двух βк и двух xg, охватывающих заданные величины. Сначала выполняется интерполяция (в данном случае среднеарифметическая) по xg (при βк=15° и 20°), затем интерполяция полученных Rгк и bопт по βк (при xg=1,5 м). Последовательность определения Rгк и bопт показана на данном примере в нижеприведенной таблице.

Если далее задаться вероятным значением полного пропульсивного КПД η, то можно оценить потребную мощность двигателя
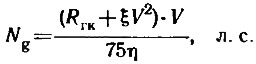
где ξ суммарный коэффициент аэродинамического сопротивления и выступающих частей.
В первом приближении можно принять η=0,6 для гребного винта и η=0,45 для водометного движителя, предварительно вычислив ξ на основе рекомендаций в упомянутых выше статьях (на примере подвесного мотора и водомета). В случае наклонных валов с кронштейнами или угловых колонок можно оценить ξ по существующим методикам, содержащимся в специальной литературе.
Подводя итог, следует напомнить, что расчетная величина bопт соответствует оптимальному расположению продольных реданов или иных брызгоотсекающих кромок, ограничивающих необходимую площадь глиссирования на выбранном режиме, и может отличаться от принятой конструктивной ширины корпуса по скуле, задаваемой условиями общего расположения или выхода на режим глиссирования.
Для выбора ширины корпуса по скуле в последнем случае необходимо соблюдать ограничение по числу Фруда Frb≥1,5, соответствующее началу устойчивого глиссирования с появлением гидродинамической составляющей подъемной силы.