Продольная устойчивость при глиссировании

При глиссировании сопротивление трения составляет от 20 до 85% общего сопротивления движению, причем с ростом скорости доля сопротивления трения увеличивается; поэтому для скоростных глиссирующих катеров выгодно задавать кормовую центровку, позволяющую уменьшить смоченную длину и поверхность и, следовательно, снизить сопротивление трения. Однако, задавая кормовую центровку, не следует забывать о том, что катер может оказаться неустойчивым на ходу.

Скорость, при которой наступает явление неустойчивости (дельфинирование), зависит от целого ряда параметров, характеризующих нагрузку, центровку и геометрические элементы корпуса глиссирующего катера.

Границу относительной скорости, при которой происходит потеря устойчивости движения, в зависимости от основных параметров корпуса глиссирующего катера удалось экспериментально установить [1] в результате анализа испытаний моделей систематической серии (серия 62). Идентичные результаты были получены и при испытаниях моделей систематической серии БК [2].

Серия 62 состояла из пяти моделей, имеющих следующие значения относительной длины (L:В max): 2,0; 3,06; 4,09; 5,5; 7,0. Каждая модель серии испытывалась в диапазоне чисел Фруда по водоизмещению Бгд = = 0,5÷6,0; коэффициент статической нагрузки С_Δ и относительная центровка x_g изменялись в весьма широких пределах. Указанные величины выражаются следующими формулами:


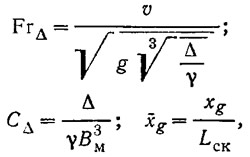
где Δ — весовое водоизмещение судна, т;
γ — удельный вес воды, т/м³;
В_м — ширина судна по скуле на миделе, м;
υ — скорость движения, м/сек;
g — ускорение силы тяжести (g = 9,81 м/сек²);


L_CK — длина катера по скуле, м;
x_g — отстояние центра тяжести от транца, м.

В процессе обработки результатов испытаний моделей вышеуказанных серий получена зависимость отношения коэффициента динамической нагрузки:


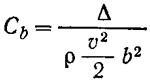
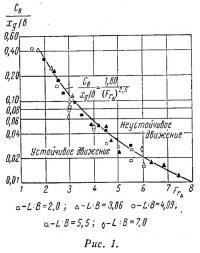
к относительной центровке x_g/b в функции от числа Фруда Fr_Δ (рис. 1). Здесь b — ширина модели (катера) в месте расположения центра тяжести. Все экспериментальные точки, при которых возникает явление неустойчивости, ложатся на одну кривую. Зачерненные фигуры на рис. 1 соответствуют границе устойчивого движения. (Некоторый разброс точек обусловлен неточностью определения момента потери устойчивости для каждого испытания). Дополнительно на графике представлены отдельные точки (незачерненные фигуры), соответствующие устойчивому движению на высоких скоростях для всех пяти моделей серии 62. Все они располагаются ниже кривой, определяющей потерю устойчивости движения.

Указанная кривая может быть аппроксимирована следующей формулой:


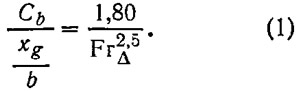
Таким образом, если левая часть формулы меньше правой, — движение катера устойчиво и наоборот, если больше — неустойчиво. После несложных преобразований формула (1) может быть представлена в следующем виде:



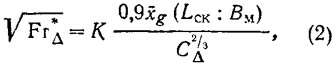
где Fr_Δ — число Фруда, при котором происходит потеря продольной устойчивости движения катера.

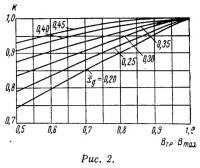
Величина численного коэффициента К, являющегося функцией от относительной центровки и сужения кормовой оконечности (В_тр:В_м), определяется по графику (рис. 2).

Таким образом, наиболее существенное влияние на величину скорости Fr_Δ, при которой катер теряет продольную устойчивость, оказывают относительная центровка, относительная длина, коэффициент статической нагрузки, а также сужение кормовой оконечности катера.

При проектировании высокоскоростных катеров, в особенности гоночных судов, режим движения которых, как правило, близок к границе потери продольной устойчивости, необходимо в каждом конкретном случае производить проверку продольной устойчивости по приведенным формуле или графику.

Литература

• 1. Е. Р. Кlеmеnt, D. L. Blount, Resistance Tests of a Sistema-tic Series of Planing Hull Forms, «Transaction of the Society of Naval Architects and Marine Engineers», Vol. 71, 1963.
• 2. М. М. Буньков, Метод расчета сопротивления остроскулых катеров, «Катера и яхты», №19.