Условия, которыми я располагаю, таковы, что зимой мне необходимо прямо в квартире сделать как можно больше заготовок, чтобы затем летом в сравнительно короткий срок (за отпуск) собрать корпус — желательно до полной готовности. Из этого следует, что все предварительно изготовленные детали и узлы должны иметь практически чистовую обработку, которую, кстати, выполнить проще именно дома, а не возле стапеля, где, как правило, не бывает верстаков, а порой и просто ровного пола. Если припуск на подгонку и нужен, то он должен быть минимальным — порядка 1—2 мм.
Известные мне технологические методы сборки любительских судов основаны на принципе «подгонки по месту», т. е. даже не предусматривают изготовления точных заготовок.
Не совсем меня устраивают и существующие методы определения необходимых размеров по плазовому чертежу. Не в каждой квартире можно разместить чертеж размером минимум 5Х2 м. После каждого сворачивания состояние его отнюдь не улучшается. Но самое главное он, как правило, не обеспечивает нужной точности — ведь начертить даже прямой угол таких размеров достаточно сложно. А что касается кривых линий, то здесь, по-моему, вообще все обстоит крайне неудовлетворительно.
Информация об изображении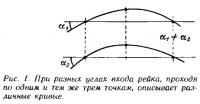
Рис. 1. При разных углах входа рейка, проходя по одним и тем же трем точкам
Поясню в двух словах, почему меня не устраивает широко рекомендуемый метод «гибкой рейки».

Рис. 1. При разных углах входа рейка, проходя по одним и тем же трем точкам
Погрешности этого метода обуславливаются, как я называю, «углом входа рейки в крайнюю точку». На рис. 1 видно, что при разных углах входа рейка, проходя по одним и тем же трем точкам, описывает совершенно различные кривые. Я уж не говорю о внутренних неоднородностях, имеющихся в каждой материальной, а не теоретической рейке!
Любителю приходится учитывать и тот факт, что даже эти точные, известные из проекта точки могут быть ошибочными хотя бы вследствие опечаток. Например, вычерчивая уже в который раз корпус своей очередной яхты и делая модель, я почти интуитивно почувствовал, что некоторые теоретические линии корпуса, например, киля, не соответствуют главному условию однородной плавности и выпуклости, без локальных перегибов. Это стало хорошо видно, когда я сжал масштаб по ватерлинии в пять раз (кстати, этот метод тоже весьма полезен для проверки -плавности «вытянутых» кривых линий). После этого сразу стало видно, что некоторые точки киля, хотя данные и взяты из таблицы плазовых ординат, «выпадают».
Нарисовав самому себе такую нерадостную картину (может быть, она существует лишь в моем разгоряченном воображении?), я начал искать методы конструирования, обеспечивающие требуемую точность при относительной простоте.
Оказалось, что такой метод давно существует в математике и называется интерполяцией, ну а конкретно я изучил и применяю так называемый интерполяционный метод Лагранжа. Несмотря на пугающее название, он не требует никаких специальных знаний, кроме обычного школьного курса алгебры и арифметики. Метод позволяет найти аналитическое выражение любой линии корпуса яхты, проходящей через некоторые заданные точки. Подставляя затем в эту формулу любое значение аргумента, можно определить координаты любых других промежуточных точек, пользуясь лишь приблизительным рисунком и простейшим калькулятором.
Из самого условия интерполирования следует, что описываемая полученной формулой линия будет идеально гладкой и единственной (см., например, книгу: Турчак Л. И. «Основы численных методов». М., Наука, 1987 г.).
Искомая формула (называемая многочленом Лагранжа) в общем виде выглядит так:
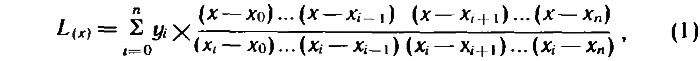
где x0, x1, х2, ... хn; у0, y1, у2, .... уn — координаты известных из проекта «точных» точек, а x и y — координаты искомой точки.
Покажу на конкретном примере, как я пользуюсь этой формулой для определения размеров практических шпангоутов яхты микрокласса «Морской кот», проект которой опубликован в «КиЯ» №99.
Пусть нас интересует полуширота линии борта практического шпангоута, размещенного на расстоянии 1275 мм от транца (предположим, что именно в этом месте по ряду соображений мы решили сделать переборку, — не нужно искать ее в проекте).
Последовательность действий такова.
- 1. Сначала определяем аналитическое выражение линии борта как функции расстояния от транца (удобнее именно от транца).
- 2. Подставляем в формулу нужное расстояние и получаем искомую полушироту.
Особенность многочлена Лагранжа такова (как, впрочем, н любого другого подобного выражения), что чем большеточек мы будем брать,тем точнее получим результат, но одновременно тем сложнее будут вычисления и окончательная формула. Конечно, в оптимальном случае нужно было бы заложить в формулу все имеющиеся в таблице плазовых ординат одиннадцать точек, но, как я уже отметил, правильность их (для меня, во всяком случае) сомнительна Поэтому лучше взять несколько (4—5) точек, равномерно размещенных по ватерлинии и находящихся на плоскостях теоретических шпангоутов; найденная линия, проходя через эти табличные точки, будет как бы автоматически выравнивать координаты остальных шпангоутов, удовлетворяя условию плавности. Поскольку эта кривая — единственная, то, видимо, именно ее и надо принять за эталон.
Если даже авторы проекта сочли нужным придать поверхностям корпуса местные искривления, то и тогда предлагаемый метод полностью применим для нахождения промежуточных координат. В этом случае в формулу нужно подставлять не все теоретические шпангоуты, а только «два слева, два справа» от выбранной точки; вся последующая работа остается без изменений.
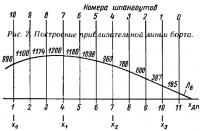
Для удобства вычислений теоретический чертеж необходимо немного преобразовать. Проведем условную горизонтальную линию — ДП и перпендикулярно к ней прочертим (можно от руки, на обычной писчей нелинованной бумаге!) все теоретические шпангоуты, от 0-го до 10-го. Пусть справа будет нос, слева — корма, а над ДП нарисуем приблизительную линию борта (см. рис. 2).
В точках пересечения шпангоутов с ДП поставим числа; для шп. № 10 — 1, для № 9 — 2 и т. д. Это будут условные единицы измерения «икс».
Точки пересечения линии борта со шпангоутами также пометим числами — значениями полу-широт, после чего отметим, на каком шпангоуте значение полушнроты максимально (1200 мм). Этот шпангоут (№ 7) принимаем за отправную точку в наших расчетах. Затем следует выбрать еще две-три равномерно отстоящих друг от друга точки, находящихся на плоскостях теоретических шпангоутов и максимально «растянутых» по всему корпусу. В нашем случае это шпангоуты № 10, 4, 1. В совокупности со шпангоутом № 7 они дадут нам четыре исходных «икса» со следующими значениями: х0=1; x1=4; х2=7; х3=10. Соответствующие этим точкам значения «игреков» будут: y0=990; y1=1200; y2=960; y3=397.
Подставив эти значения «иксов» и «игреков» в формулу (1) и упростив выражение, получим:
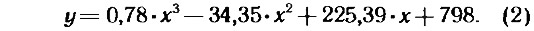
Подставляя в формулу в качестве проверки вместо x последовательно 1, 4, 7, 10, мы должны получить соответственно y: 990, 1200, 960, 397.
Вычислив значения у для остальных шпангоутов, увидим, насколько наша теоретическая линия не совпадает с предлагаемой проектом. Расхождения будут, и довольно значительные (для шпангоутов № 0, 2, 3, 5, 6, 8, 9 соответственно — 25, 13, 14, —16, —16, 12, 18).
Получив такие аналитические плазовые ординаты, судостроитель должен решить - будет ли он впредь брать их за основу или же оставит прежние, проектные. И в том и другом случае для определения промежуточных значений — размеров практических шпангоутов можно пользоваться этим же методом, только в последнем случае для каждой зоны между двумя шпангоутами придется вычислять «местную» формулу по четырем окрестным точкам. В результате будет достигнута абсолютная точность и полное соблюдение всех проектных особенностей корпуса.
Разумеется, все вычисления лучше производить с помощью калькулятора, причем владельцы программируемых калькуляторов (БЗ-34, МК-52, МК-61), составив несложную программу, смогут превратить эти расчеты в сплошное удовольствие.
Предложенный А. Устюжаниным метод аппроксимации характерных линий теоретического чертежа судна полиномами Лагранжа полезен и может быть использован проектантами при разработке обводов судна, уточнении таблицы плазо-вых ординат в качестве вспомогательного инструмента наряду с другими интерполяционными формулами.
Судостроителям-любителям можно рекомендовать использовать описанную процедуру для уточнения плазовых ординат хорошо согласованного теоретического чертежа и получения ординат ромежуточн х практических шпангоутов.
В качестве самостоятельного метода сглаживания обводов вновь проектируемого судна метод вряд ли приемлем, так как при его использовании возникнут серьезные вычислительные трудности аппроксимации трехмерной поверхности.
Появление погрешности, на которую обратил внимание автор, можно попытаться объяснить неточностью подстановки в формулу 1 исходных данных: при первой производной, равной нулю, получим х1—х0=х0—х0=0 и т. д., что приводит к необходимости исключить первый член суммы с произведением, содержащим у0.
С методами преобразования (линейного и нелинейного) теоретического чертежа можно ознакомиться, например, в журнале «Hansa» №108, 1971, стр. 2185—2188.