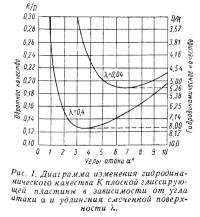
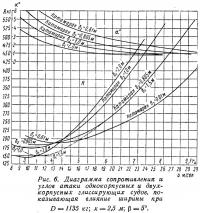
Из спортивной практики известно, что в ряде случаев глиссирующие многокорпусные суда оказываются быстроходнее однокорпусных при равных водоизмещении и мощности. На первый взгляд это кажется парадоксом. В самом деле, ширина днища однокорпусного судна значительно больше ширины каждого из корпусов катамарана или тримарана. В то же время известно, что большее удлинение1 λ смоченной поверхности днища позволяет получить большее гидродинамическое качество2 судна К. Например, как видно из рис. 1, наибольшее гидродинамическое качество плоской пластины при λ = b/l = 0,4 равно 8, а при λ = 0,04 оно равно 5,25.
Однако если мы рассмотрим углы атаки, при которых качество данных пластин достигает своей наибольшей величины, то увидим, что пластина с λ = 0,4 сможет достичь качества К = 8 только при угле атаки α = 4°, a для пластины с λ = 0,04, угол атаки, соответствующий К = 5,25, равен α = 6°30'. Из рис. 1 видно также, что пластина с λ = 0,4 при α = 1° будет обладать качеством не более 4 и при движении под этим углом атаки окажется менее выгодной, чем пластина с λ = 0,04, идущая под α = 6°30'. Отсюда следует, что вопрос о наиболее выгодном удлинении в конкретных условиях нельзя рассматривать вне связи с углами атаки. В этом и кроется объяснение того, что корпус с меньшим удлинением может оказаться выгоднее корпуса с большим удлинением.
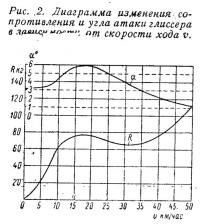
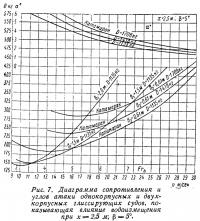
Всегда желательно, чтобы на расчетной (наибольшей) скорости судно шло под наивыгоднейшим углом атаки. Однако при сравнительно больших удлинениях однокорпусных глиссеров это не всегда выполнимо, так как при наивыгоднейших углах атаки (4—5°) ход судна становится неустойчивым: отрываясь от воды и затем падая, судно испытывает непрерывные удары, что снижает его скорость. Приходится мириться с тем, что фактические углы атаки на расчетных скоростях значительно меньше наивыгоднейших (1—1,5°). Правда, к ходу под столь малыми углами атаки на наибольших скоростях вынуждает еще одно обстоятельство. С ростом скорости гидродинамическая подъемная сила при неизменном угле атаки растет пропорционально квадрату скорости, т. е. гораздо быстрее, чем падает ввиду всплывания судна архимедова сила поддержания. Чтобы суммарная поддерживающая сила оставалась всегда равной весу судна, необходимо замедлить рост гидродинамической силы, уменьшая углы атаки по мере роста скорости. Это происходит «автоматически», если центровка судна неизменна. На рис. 2 показаны типичные кривые сопротивления и углов атаки глиссирующего однокорпусного судна в зависимости от скорости хода. С ростом скорости выше вершины «горба» кривой сопротивления и гидродинамической подъемной силы судно всплывает, смоченная длина сокращается, от чего уменьшается момент гидродинамической подъемной силы, дифферентующий на корму, и падает угол атаки. Заметим, что увеличение упора винта с возрастанием скорости существенного влияния на дифферент в большинстве случаев не имеет.
Посмотрим теперь, что произойдет, если уменьшить ширину днища глиссера. Из рис. 1 видно, что с уменьшением удлинения при сохранении неизменного качества угол атаки увеличивается. Одновременно с этим увеличиваются погружение и смоченная длина днища. Однако несмотря на увеличение угла атаки, устойчивость хода не нарушается, так как чем больше по сравнению с шириной днища смоченная длина и, следовательно, расстояние от транца до центра давления (отношение x/b), тем выше скорость, при которой возможна потеря устойчивости.
Можно подобрать удлинение днища и скорость хода так, что гидродинамическое качество получится более высоким, чем у широкого (первоначального) днища, идущего под меньшим углом атаки. Так, например, если при первоначальном удлинении днища λ = 0,4 угол атаки составлял 1°, а после сужения днища (λ=0,04) угол атаки стал равен 5°, то качество повышается с 4 до 5. Однако уменьшить ширину однокорпусного судна часто оказывается практически невозможным (например, из соображений остойчивости), поэтому ширина днища однокорпусных глиссирующих судов большей частью превышает наивыгоднейшую. Многокорпусные же суда представляют гораздо больше возможностей для уменьшения ширины днища до вчения, соответствующего наивыгоднейшему качеству при данной скорости.
Для решения вопроса о целесообразности (с точки зрения ходкости) постройки многокорпусного судна следует определить для заданной скорости хода наивыгоднейшую ширину однокорпусного и многокорпусного судов и рассчитать их сопротивления. В случае неприемлемости наивыгоднейших ширин следует задать наименьшие возможные ширины и вновь вычислить сопротивление обоих судов.
Проиллюстрируем Это на численных примерах.
Пример 1. Требуется выяснить качество однокорпусного и двухкорпусного судов при следующих условиях. Водоизмещение D = 1135 кг; центр тяжести расположен в нос от транца на расстоянии х = 2,5 м; угол килеватости (β = 5°; расчетная скорость υ = 48 км/час = 13,4 м/сек.
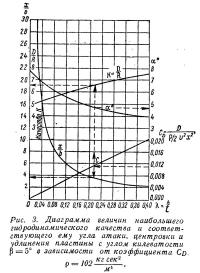
1. Пользуясь графиком на рис. 3, определяем наивыгоднейшую ширину однокорпусного судна. Для этого вычисляем величину коэффициента СD:
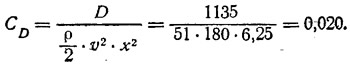
Этому значению Со соответствует (по горизонтальной шкале) значение λ = 0,388.
2. По кривой x/b найденному значению λ соответствует значение х/b = 2, откуда находим наивыгоднейшую ширину b1:
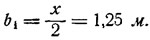
3. Тому же значению λ = 0,388 на кривой качества K = D/R соответствует значение К = 7,5, откуда находим, что сопротивление R при заданной скорости υ = 13,4 м/сек равно 1135:7,5 = 150 кг.
4. По кривой углов атаки а для λ = 0,388 находим соответствующий угол атаки α = 3°50'.
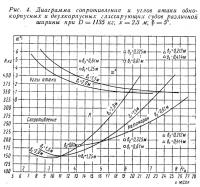
Найденные величины отмечены на рис. 4 круглыми точками на скорости υ = 13,4 м/сек.
Вычислим теперь наивыгоднейшую ширину двухкорпусного судна и соответствующее его сопротивление.
Для этого пользуемся тем же графиком на рис. 3, полагая водоизмещение одного корпуса равным D/2.
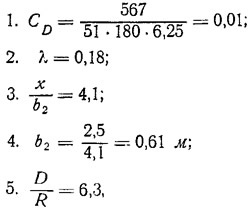
откуда сопротивление каждого корпуса:
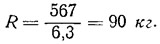
Полное сопротивление R = 90Х2 = 180 кг.
6. α = 4°50'.
Очевидно, что в данном случае однокорпусное судно будет выгоднее двухкорпусного. Найденные для катамарана величины также отмечены на рис. 4 круглыми точками на скорости υ = 13,4 м/сек.
Пример 2. Допустим, что ширина b1 = 1,25 м однокорпусного судна неприемлема и что наименьшая возможная ширина — 1,5 м; желательна же ширина 2,0 м. Требуется определить, будет ли однокорпусное судно и при этих ширинах выгоднее двухкорпусного.
Пользуясь для определения сопротивления одним из существующих методов, построим на рис. 4 соответствующие кривые сопротивления, которые покажут, что на скорости υ = 13,4 м/сек однокорпусное судно шириной b1 = 1,5 м выгоднее двухкорпусного судна шириной b2 = 0,61 М, а судно шириной b1 = 2,0 м обладает таким же качеством, что и двухкорпусное.
Пример 3. Требуется определить, какой тип судна будет обладать большим гидродинамическим качеством при тех же условиях, что и в предыдущих двух примерах, ко при скорости хода υ = 19 м/сек = 68,5 км/час.
Пользуясь теми же средствами, что и при решении примеров 1 и 2, найдем, что наивыгоднейшей для новой скорости шириной однокорпусного судна является b1 = 0,61 м, а для двухкорпусного b2 = 0,325 м. При этих условиях, как видно из рис. 4 (квадратные точки на скорости υ = 19 м/сек), при наивыгоднейших ширинах судов и при скорости 68,5 км/час большим качеством будет обладать однокорпусное судно.
Однако в случае, если ширина однокорпусного судна b1 = 1,5 м, а не 0,61 м, то большим качеством будет обладать двухкорпусное судно, имеющее b2 = 0,325 м и b2 = 0,61 м или несколько больше. Если же ширина однокорпусного судна b1 = 2,0 м, то качество двухкорпусного судна при b2 = 0,61 м будет больше примерно на 30%, чем однокорпусного.
Если мы произведем аналогичные вычисления для скорости υ = 24 м/сек, то, как видно из рис. 4 (треугольные точки), получим ответ качественно такой же, как и для скорости 19 м/сек, т. е. что при наивыгодкейших ширинах наибольшим качеством будет обладать однокорпусное судно, а при ширине b1 = 1,5 м — двухкорпусное, имеющее b2 = 0,61 м.
Эти заключения справедливы, если более выгодное судно будет обладать устойчивым ходом. Для суждений об устойчивости хода можно пользоваться диаграммой на рис. 5, предложенной Штольцем. Показателем степени устойчивости хода здесь является отношение x/b в зависимости от коэффициента нагрузки:
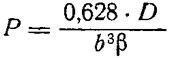
Сплошная кривая дает минимальное значение величины x/b, необходимое для устойчивости хода, а пунктирная — гарантирующее значение. Как видим, чем больше угол килеватости β, тем более кормовой может быть центровка; чем больше водоизмещение данного судна, тем дальше к носу должен быть расположен ЦТ, чтобы ход был устойчивым. Практически, если отношение x/b ≥ 1,25, можно не опасаться за устойчивость хода. В наших примерах x = 2,5 м, а наибольшая ширина b1 = 2,0 м, откуда x/b1 = 1,25. В других же случаях ширина значительно меньше, ввиду чего ход судов будет заведомо устойчивым.
Приведенные примеры показывают, что чем больше скорость хода, тем больший выигрыш в сопротивлении можно получить на двухкорпусном судне. Действительно, катамаран, у которого b2 = 0,61 м, по сравнению с однокорпусным судном шириной b1 = 1,5 м при скорости υ = 13,4 м/сек имеет сопротивление на 15% большее, при υ = 19 м/сек — на 10% меньшее, а при υ = 24 м/сек — на 20% меньшее.
На диаграмме на рис. 6 приведены кривые сопротивления и углы атаки для однокорпусных судов шириной 1,5 и 2,0 м и двухкорпусных судов различной ширины. На этой диаграмме отчетливо видно преимущество однокорпусных судов на малых скоростях (до FrΔ = 4÷5) и преимущество двухкорпусных на больших.
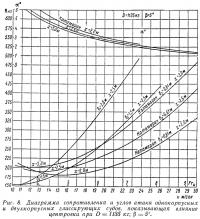
Конструкция двухкорпусных судов часто оказывается более тяжелой, чем однокорпусных. Ввиду Этого представляет особый интерес диаграмма на рис. 7, на которой сравниваются кривые сопротивления двухкорпусного судна при различных нагрузках. По мере роста скорости относительное увеличение сопротивления от перегрузки падает.
На двухкорпусных судах больше возможностей выбирать место расположения ЦТ по длине, чем на однокорпусных. На рис. 8 сравниваются кривые сопротивления двухкорпусного судна при различных центровках. Чем больше скорость, тем большего эффекта можно добиться, смещая ЦТ к корме.
Преимущество двухкорпусного судна по сравнению с однокорпусным на больших скоростях хода может быть еще большим, если увеличить длину судна и расстояние между корпусами, так как при соответствующих профилировке и размерах палубы аэродинамический эффект близости уровня воды (экрана) может существенно увеличить аэродинамическую подъемную силу судна.
1. Удлинением λ будем называть отношение ширины днища b к длине смоченной поверхности l, то есть λ = b/l.
2. Гидродинамическим качеством K будем называть отношение полной подъемной силы днища, численно равной водоизмещению D, к полному гидродинамическому сопротивлению R, то есть K = D/R.