Особенности расчета катерных гребных винтов

Проектирование гребных винтов для быстроходных катеров имеет ряд специфических особенностей. Далеко не всегда конструктор располагает надежной кривой буксировочного сопротивления, так как испытания моделей катеров в опытовом бассейне проводятся довольно редко. Еще сложнее учесть влияние на сопротивление катера и условия работы двигателя и винта волнения (начиная с высоты волны 0,5—0,7 м) и ветра. Во многих случаях гребные валы располагаются наклонно, что приводит к косому обтеканию винтов, которое вызывает более раннее наступление кавитации и падение упора винта. Катерные двигатели имеют жесткую характеристику, не допускающую практически никакой перегрузки.

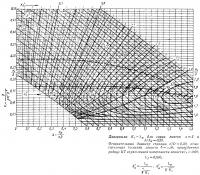
При использовании для расчета катерных гребных винтов широко распространенных экспериментальных диаграмм (Трооста, Тейлора и т. п.) учесть указанные особенности не удается. Эти экспериментальные диаграммы построены на основании испытаний моделей малооборотных («тихоходных») гребных винтов в довольно узком диапазоне удельных нагрузок и зачастую совершенно неприемлемы для расчета кавитирующих «быстроходных» винтов с относительно малой поступью. Поэтому в практике расчета катерных винтов чаще применяют диаграммы Э. Э. Папмеля, которые построены не на базе обработки результатов модельных испытаний, а получены расчетным путем применительно к полноразмерным винтам. Эти диаграммы обеспечивают широкое изменение элементов винтов и позволяют проектировать как некавитирующие, так и кавитирующие гребные винты.

Коэффициенты взаимодействия винта и корпуса

Значение коэффициента попутного потока для водоизмещающих катеров может быть достаточно точно определено по формуле Э. Э. Папмеля:



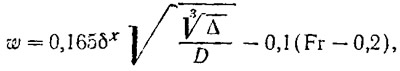
где δ — коэффициент общей полноты катера;
х = 1 — для винтов, расположенных в ДП, и х = 2 — для бортовых винтов;
Δ — водоизмещение, м³;
D — ожидаемый диаметр гребного винта, м;
Fr —- число Фруда.

Коэффициенты влияния неравномерности попутного потока на упор, момент и к. п. д. при наличии достаточных зазоров между винтом, корпусом и кронштейном вала могут быть приняты равными i₁=i₂=i=l.

Коэффициент засасывания на швартовых в зависимости от обводов корпуса и расположения гребного винта принимается равным:


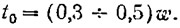
На рабочем режиме коэффициент засасывания:


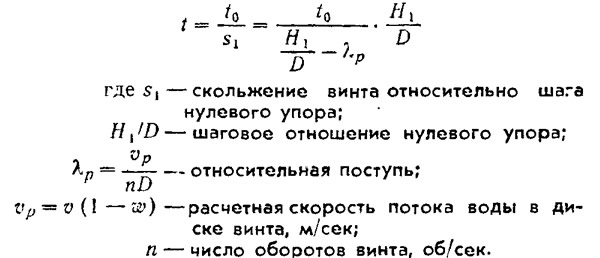
У глиссирующих катеров и катеров на подводных крыльях попутный поток и сила засасывания практически отсутствуют, так как винты обтекаются почти невозмущенным потоком воды, однако в этом случае необходимо учесть влияние косого обтекания винта. При отсутствии кавитации можно принять, что наклон гребного винта к потоку приводит к уменьшению расчетной скорости обтекания до величины υ cos θ и снижению полезного упора P до величины P cos θ, где θ — угол наклона вала гребного винта. По аналогии с водоизмещающими катерами, количественный учет уменьшения скорости обтекания и упора винта целесообразно производить при помощи условных коэффициентов попутного потока ω и засасывания ι:



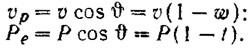
Численные значения этих коэффициентов могут быть определены по формуле, рекомендованной М. Н. Веселовским:


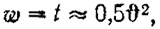
в которой угол скоса потока в радианах равен:


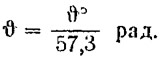
Под углом скоса потока при определении ω обычно понимается угол между осью вала и днищем или кормовым крылом катера, а при определении t — угол между осью вала и поверхностью воды с учетом ходового дифферента.

При более точных расчетах следует учитывать возникающую при косом обтекании поперечную силу, расположенную в плоскости диска винта и направленную вверх. Одна составляющая этой силы вызывает разгрузку катера, благодаря чему сопротивление катера уменьшается. Другая составляющая направлена в сторону, противоположную движению, и приводит к увеличению сопротивления.

Потери мощности на трение в валопроводе и редукторе

Потери мощности на трение валопровода в опорных и упорном подшипнике, сальнике дейдвуда и редукторе обычно учитываются суммарным механическим к. п. д. η_м:



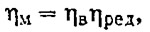
где η_в = 0,96÷0,98 — к. п. д. валопровода;
η_ред = 0,96÷0,98 — к. п. д. редуктора, вводимый, если мощность двигателя указана без учета редуктора.

Выбор числа лопастей и дискового отношения винта

Число лопастей некавитирующих гребных винтов выбирается в зависимости от величины коэффициентов r_n или r_d, вычисленных для ожидаемом максимальной скорости и характеризующих нагрузку винта. При слабонагруженных винтах, когда:


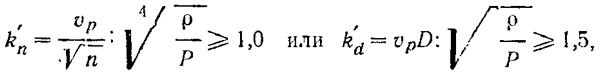
число лопастей принимается равным z = 3. Если величины этих коэффициентов меньше указанных (при большой нагрузке), применяются четырехлопастные винты.

Кавитирующие гребные винты с целью отдаления начала кавитации и ослабления ее влияния обычно проектируются трехлопастными.

В последнее время имеются случаи применения на быстроходных катерах пяти- и даже шестилопастных кавитирующих винтов. Это приводит к некоторому снижению максимальной скорости хода, зато уменьшает нежелательные вибрации кормовой оконечности.

Величина дискового отношения некавитирующих гребных винтов должна выбираться таким образом, чтобы на наиболее длительных эксплуатационных режимах исключались возникновение кавитации и появление эрозии гребных винтов.

Предварительно можно принимать:



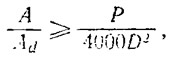
где Р — упор винта на режиме полного хода, кг;
D — ожидаемый диаметр винта, м.

В дальнейшем величина А/А_d уточняется поверочным расчетом на кавитацию. В тех случаях, когда не удается избежать наступления кавитации даже при увеличении А/А_d до 1—1,2, следует переходить на проектирование кавитирующих винтов.

Для кавитирующих гребных винтов обычно принимается А/А_d=0,9÷1,2.

Расчет гребного винта при помощи диаграммы Э. Э. Папмепя

В большинстве случаев конструктору при расчете гребного винта приходится исходить из заданных значений мощности двигателя и числа оборотов; часто бывает ограничен и диаметр гребного винта. В этих условиях расчетом определяются наибольшая достижимая скорость катера, шаговое отношение и к. п. д. винта.

Схема расчета некавитирующего гребного винта для этого случая приведена в табл. 1. Следует заметить, что при скорости до 40 км/час и числе оборотов гребного вала 1500—2000 об/мин гребные винты обычно не кавитируют, поэтому приводимой схемой можно пользоваться практически для любых катеров с конвертированными автомобильными двигателями мощностью до 100 л. с.


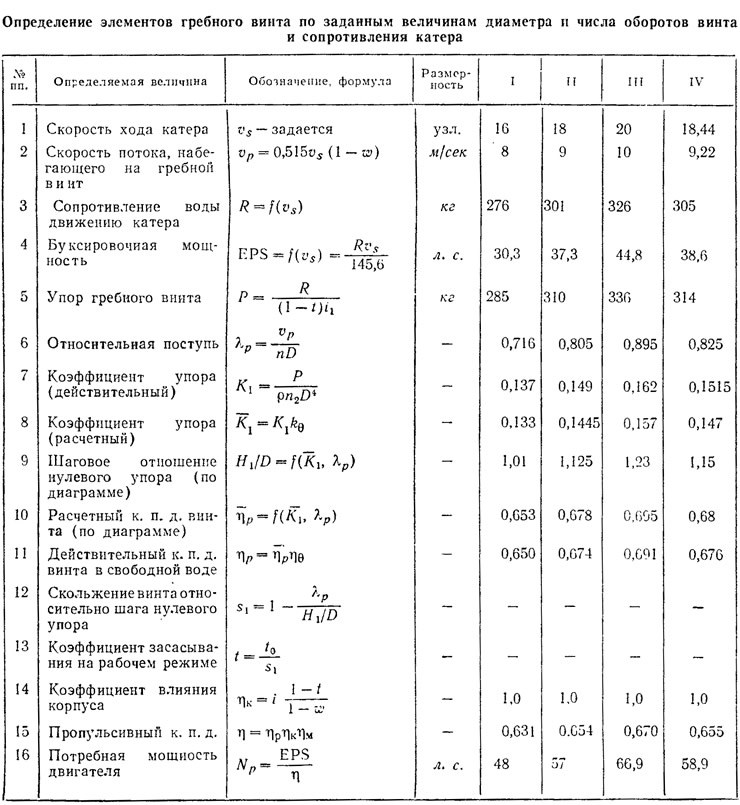
Расчет можно вести в виде последовательных приближений, задаваясь скоростью хода катера υ_s (первая строка расчетной таблицы). Если в начале расчета коэффициент засасывания на рабочем режиме неизвестен, то для первого приближения его необходимо определить пробным расчетом. Для всех же последующих приближений значение коэффициента t берется из столбца предыдущего приближения (строка 13).


В результате расчета на диаграмме Э. Папмеля находится точка действия винта, определяемая значением относительно поступи λ_p на оси абсцисс Диаграммы) и коэффициентом упора:


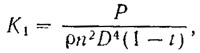
где ρ — массовая плотность воды.

Приводим наиболее употребительную диаграмму для расчета некавитирующих трехлопастных винтов с A/A_d = 0,55. Более широко такого рода диаграммы представлены в атласе Э. Э. Папмеля, входящем в его книгу «Практический расчет гребного винта», а также в приложении к книге М. М. Жученко и В. М. Иванова «Расчеты гребных винтов».

Если число лопастей z_расч и дисковое отношение θ_расч проектируемого винта не совпадают с их диаграммными значениями (z_диагр. θ_диагр.). то для возможности использования имеющихся Диаграмм в расчет вводятся переходные коэффициенты:


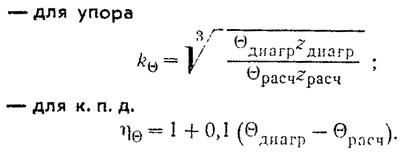
Расчет считается законченным пои совпадении значений располагаемой мощности двигателя и потребной мощности, полученной в строке 16, а также при совпадении значений коэффициента засасывания l, принятого в строке 5 и полученного в строке 13.

Для того чтобы избежать перегрузки двигателя во время эксплуатации катера вследствие обрастания корпуса, действия волнения и т. п., расчет винта следует выполнять при условии использования 90—95% всей располагаемой мощности при максимальном числе оборотов двигателя.

В диаграммах Э. Папмеля принято в качестве определяющего параметра не конструктивное шаговое отношение H/D, а шаговое отношение нулевого упора H/D, являющееся важнейшей гидродинамической характеристикой. К конструктивному шаговому отношению можно перейти при помощи формулы:


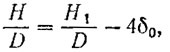
где δ₀ — относительная кривизна средней линии профиля сечения лопасти на радиусе R₀.

Для иллюстрации изложенных методов приведем пример определения скорости хода и элементов гребного винта (см. таблицу) небольшого одновинтового глиссирующего катера водоизмещением 1,48 т.

Угол наклона оси гребного вала к поверхности воды 9°30'; угол между осью вала и днищем 4°; ходовой дифферент 4°. Данные углы определяют следующие условные коэффициенты взаимодействия винта и корпуса:


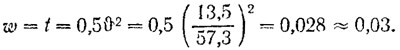
Глубина погружения оси гребного винта h_s ≈ 0,5 м.
Максимально допустимый диаметр гребного винта D = 0,4 м.

Устанавливается главный двигатель «М51-УМ» с длительной эксплуатационной мощностью N_e=62 л. с. при числе оборотов n_дв=2600 об/мин. Для обеспечения необходимого запаса числа оборотов расчет элементов гребного винта ведется на уменьшенную мощность N_p=0,95 N_e=59 л. с.

Коэффициент редукции числа оборотов i_p=1:1,55; таким образом, число оборотов винта n=27,95 об/сек. К. п. д. валопровода η_в=0,97.

Поскольку коэффициент «числа оборотов — упора» k_n превышает 1 и винт является малонагруженным, число лопастей принимаем равным z=3.

Диаметр винта принимается равным максимально допустимому D=0,4 м; это примерно на 10 мм больше оптимального значения и в дальнейшем позволит производить доводку гребного винта на испытаниях путем обрезки диаметра без снижения к. п. д. Дисковое отношение соответственно должно быть несколько более определенного по формуле:


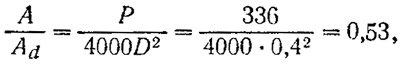
поэтому принимаем его равным A/A_d=0,6.

Поскольку коэффициент засасывания на рабочем режиме нам известен (t=0,03), строки 12 и 13 не заполняются.

Значения сопротивления R для интересующего нас диапазона расчетных скоростей υ_s снимаем с имеющихся в нашем распоряжении кривых, построенных по результатам испытаний, и проставляем в строке 3. Значения расчетного к. п. д. винта и шагового отношения нулевого упора снимаются с диаграммы К₁ — λ_p для трехлопастных винтов с дисковым отношением A/A_d— 0,55. Переходные коэффициенты ввиду несовпадения расчетного и диаграмного дискового отношения будут составлять: k_θ=0,97; η_θ=0,995.

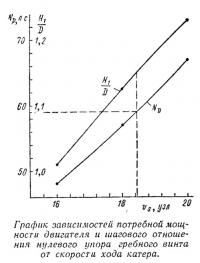
По результатам расчета построен график зависимостей мощности двигателя и шагового отношения нулевого упора винта от скорости хода, позволяющий определить, что при мощности N_р=59 л. с. наибольшая достижимая скорость хода составит около 18,4 узла. Шаговое отношение нулевого упора при этом будет равно 1,15. Для проверки правильности произведенного расчета в столбце 4 таблицы выполнен контрольный расчет, результаты которого уточняют все элементы и характеристики проектируемого винта.

Принимая относительную кривизну средней линии профиля δ₀=0,03, находим конструктивное шаговое отношение:

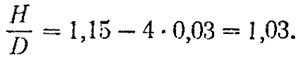
Проверка винта на кавитацию

После определения наибольшей скорости хода и основных элементов гребного винта необходимо проверить его на отсутствие кавитации. Проверка производится путем сравнения критического числа оборотов винта, при котором возникает кавитация на эквивалентном элементарном профиле, расположенном на радиусе г₀ центра тяжести спрямленной поверхности лопасти и имеющем толщину е и ширину b_ср, с действительным числом оборотов на максимальной скорости хода.

При нормальных образованиях лопасти:


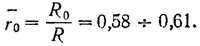
Обычно необходимые сведения об относительной толщине лопасти δ', приведенном радиусе г₀ и других элементах винта приводятся на поле расчетной диаграммы. В первом приближении можно принять:


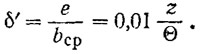
Определение критического числа оборотов для выбранных элементов винта производится в следующем порядке.

1. Находится относительная поступь винта для расчетной скорости:


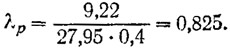
2. Вычисляется или снимается с диаграммы коэффициент упора:


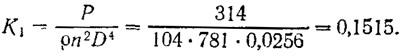
3. Определяется коэффициент подъемной силы эквивалентного профиля:


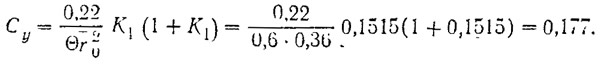
4. Находятся функции угла поступи винта β:


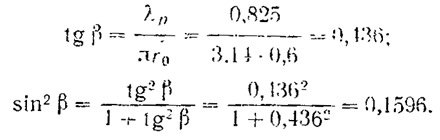
5. Вычисляются параметр 1 — φ_∞ и критическое число кавитации χ_к:


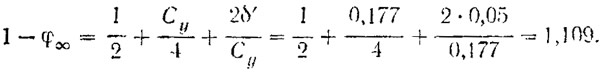
В данном случае принимается δ'=0,05.


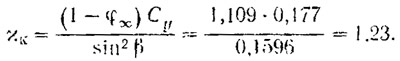
6. Рассчитывается действительное число кавитации:


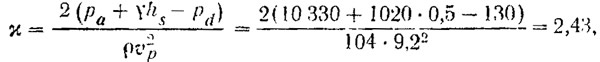
где p_a = 10330 кг/м² — атмосферное давление;
γ = 1020 кг/м³ — объемный вес морской воды;
p_d = 130 кг/м² — давление насыщенных паров воды при температуре 12° С.

7. Определяются критическое число оборотов винта и запас на кавитацию:


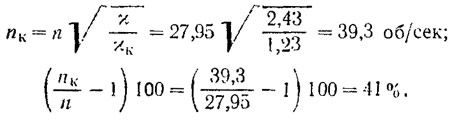
Таким образом, запас числа оборотов против наступления кавитации составляет 41%.

Учитывая, что в данном случае винт работает в скошенном потоке, полученный запас числа оборотов можно считать нормальным. Обычно же для полной гарантии в отсутствии кавитации (как ее первой стадии, сопровождающейся эрозией винта, так и второй, вызывающей падение упора и к. п. д. винта) необходимо, чтобы запас числа оборотов составлял не менее 20—30%. Если это условие не удовлетворяется, необходимо уменьшить относительную толщину эквивалентного профиля δ' или увеличить ширину сечений лопасти b и повторить весь расчет. Если же этими мерами кавитацию предотвратить не удается, следует выполнять расчет с учетом кавитации. Расчет кавитирующих винтов с учетом косого обтекания будет рассмотрен в одном из ближайших выпусков сборника.