Уравновешивание гоночных подвесных моторов

Как известно, при работе двигателя в движущихся частях кривошипного механизма возникают силы инерции. Эти силы являются основной причиной вибрации двигателя и вызывают появление знакопеременных нагрузок в отдельных его деталях, что приводит к усталости материала этих деталей, а иногда и их поломке. Поэтому уравновешивание гоночных подвесных моторов (ГПМ) является основным путем для повышения их надежности.

Прежде чем приступить к рассмотрению конкретных примеров уравновешивания ГПМ, напомним некоторые основные понятия из кинематики и динамики шатунно-кривошипного механизма поршневого двигателя внутреннего сгорания.

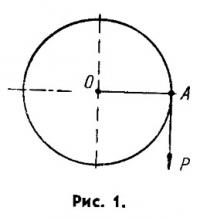
Если в точке О мы имеем вал (рис. 1) с кривошипом О А и если в точке А приложено усилие Р, направленное касательно к окружности, описываемой при вращении точкой А, то крутящим моментом М называется произведение усилия на плечо:


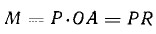
где R = О А, т. е. R — радиус кривошипа.


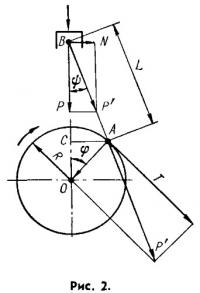
Обращаясь к рис. 2, мы видим, что сила давления газов на поршень Р, действующая по оси цилиндра, передается через шатун ВА пальцу кривошипа. Угол φ представляет переменный угол поворота кривошипа в данный момент. Угол наклона шатуна обозначим через ψ.

Сила Р, действующая по оси цилиндра, может быть разложена по правилу параллелограмма на две силы: силу Р', действующую вдоль шатуна, и горизонтальную силу N давления на зеркало цилиндра. Тогда:


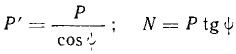
Силу Р', в свою очередь, разложим на касательное усилие в пальце кривошипа Т и усилие, направленное по радиусу:


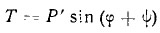
Для определения величины касательного усилия на пальце кривошипа необходимо знать:

1) переменную силу давления газов на поршень;

2) вес частей кривошипного механизма;

3) переменную силу инерции движущихся частей кривошипного механизма.


Давление газов определяется при тепловом расчете двигателя. Вес частей шатунно-кривошипного механизма определяется по геометрическим размерам деталей и плотности их материала или взвешиванием. Переменную силу инерции определяют путем динамического расчета шатунно-кривошипного механизма.

Поршень двигателя, перемещаясь от в. м. т. к н. м. т. и обратно, развивает в каждый данный момент определенную скорость, величина которой зависит от скорости вращения кривошипа и угла его поворота.

Переменная скорость, определяемая для каждого момента вращения кривошипа, называется истинной скоростью. Максимальная ее величина определяется выражением:


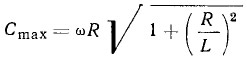
R — радиус кривошипа, м;
L — длина шатуна, м;
ω — угловая скорость вращения град/сек;


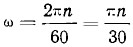
n — число оборотов коленчатого вала, об/мин. Средняя скорость поршня является величиной, получаемой из выражения:


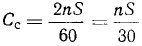
S — ход поршня.



Под ускорением поршня подразумевается изменение его скорости в единицу времени. Ускорение выражается следующей формулой:


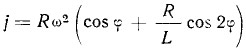
Если считать шатун бесконечно длинным, то R/L можно считать равным нулю. Тогда j = Rω² cosφ; ускорение поршня в данном случае достигает наибольшей величины в в. м. т. и н. м. т. В этих точках оно равняется Rω², а по середине хода равно нулю.

Для шатуна конечной длины в в. м. т. при φ = 0:


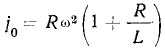
а в н. м. т. при φ=180°:


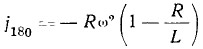
Пример 1. Определим максимальную и среднюю скорости и максимальное ускорение поршня при n=10000 об/мин; S = 2R = 60 мм и:



Сила инерции движущихся частей математически выражается как произведение массы движущегося тела на его ускорение, взятое с обратным знаком, т. е. К = —Mj, где М — масса движущихся частей. Масса, в свою очередь, выражается как М = G/g , причем G — вес частей, а g — ускорение силы тяжести, равное 9,81 м/сек².

Сила инерции прямолинейно движущихся частей создается от ускорения массы деталей, входящих в поршень, и верхней части шатуна в течение короткого промежутка времени, соответствующего примерно ‘At оборота коленчатого вала.

Когда скорость поршня увеличивается, сила инерции направлена навстречу направлению его движения, а когда уменьшается — в сторону его движения. Когда скорость достигнет максимальной величины (и вплоть до начала ее уменьшения), сила инерции равна нулю.


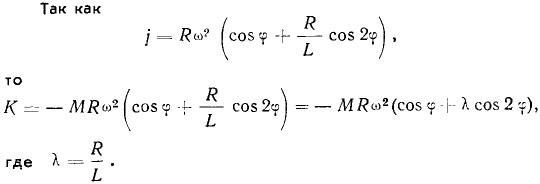
В в. м. т. φ = 0°; К₀ = —MRω² (1 + λ). Сила инерции берется со знаком минус при ее противодействии вращению коленчатого вала и с плюсом, когда она способствует его вращению.

Пример 2. Пусть вес прямолинейно движущихся частей ГПМ («Ураган-175») равен 0,276 кг; R = 0,03 м; п= 10000 об/мин;



Этот пример показывает, что инерционные силы достигают больших значений, в связи с чем они и могут вызвать вибрацию мотора и корпуса судна.


В том случае, когда силы инерции движущихся частей взаимно уравновешиваются, неподвижные части двигателя не испытывают никаких инерционных усилий. Однако, если силы инерции движущихся частей не уравновешиваются внутри двигателя, неподвижные части последнего также приходят 8 неравномерное колебательное движение, что приводит к возникновению в них инерционных сил, равных по величине и противоположных по знаку силам, возникающим в движущихся частях.

Обозначив в формуле, выражающей силу инерции,


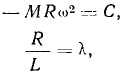
Получим:


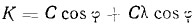
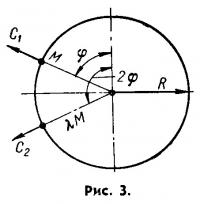
Первое слагаемое называется силой инерции первого порядка; второе — силой инерции второго порядка. Каждое из этих слагаемых может быть представлено как проекция двух векторов С = С₁ и Сλ = С₂ на ось цилиндра (рис. 3), причем вектор С₁ вращается с угловой скоростью ω, а вектор С₂ — со скоростью 2ω. Вектор C₁ может быть представлен как действующая по кривошипу ОА центробежная сила массы, равной массе прямолинейно движущихся частей поршневой группы данного цилиндра. В этом случае масса рассматривается сосредоточенной на оси кривошипе (точка А). То, что C₁ является центробежной силой, вытекает из основного положения о центробежной силе:


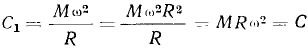
Точно так же для вектора С₂ находим:


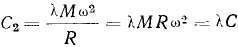
Кроме действия прямолинейно движущихся частей, следует считаться с действием центробежных сил инерции, возникающих от вращения масс, расположенных на коленчатом валу. Такая центробежная сила может быть выражена как:


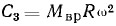
где M_вр — масса вращающихся деталей.

Центробежные силы инерции всегда направлены через ось вращения коленчатого вала и центр тяжести вращающихся масс деталей кривошипа к периферии, т. е. являются силами первого порядка, и остаются неизменными при данной угловой скорости ω.

Для уравновешивания сил инерции движущихся частей на практике используются противовесы.

Рассмотрим возможности уравновешивания одноцилиндрового двигателя ГПМ. В этом двигателе нам необходимо уравновесить:

а) силы инерции первого порядка


б) силы инерции второго порядка (детали, совершающие сложные движения)


в) силы инерции вращающихся масс первого порядка С₃ = М_врRω²; разложив их на две составляющие, получим:


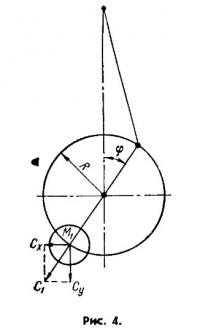
Сила С₁ может быть уравновешена противовесами коленчатого вала. Если укрепить на радиусе R массу М₁ то вертикальная составляющая центробежной силы противовеса (рис. 4) будет равна C_y = MRω²cosφ и направлена в сторону, противоположную направлению сил инерции первого порядка. Но зато получается свободная горизонтальная составляющая C_x = MRω²sinφ. По существу же, здесь сила первого порядка не уничтожена, а только смещена по времени и в плоскость, перпендикулярную оси цилиндра.

Можно поставить противовес с размерами, соответствующими M/2. Тогда будет уравновешена половина сил инерции первого порядка, что уже несколько лучше, хотя полностью задачу не решает.

Силы инерции второго порядка С₂ сохраняются полностью.

Центробежная сила С₄ уравновешивается полностью постановкой соответствующих противовесов на направление того же радиуса (только с противоположной стороны).

Из вышесказанного следует:

а) одноцилиндровый двигатель с одним кривошипом полностью уравновесить (практически) невозможно;

б) двухцилиндровый двигатель с апозитивным расположением цилиндров и одновременной их работой может быть уравновешен полностью;

в) двухцилиндровый двигатель с рядным расположением цилиндров и чередованием работы 180° уравновешивается удовлетворительно;

г) двухцилиндровые двигатели рядный с чередованием работы 0° и с апозитивным расположением цилиндров и чередованием работы 180° можно рассматривать как два одноцилиндровых двигателя с чередованием работы 0°, т. е. их уравновешенность хуже, чем одноцилиндрового двигателя.

Пример расчета уравновешивания

Произведем предварительный расчет уравновешивания шатунно-кривошипного механизма ГПМ «Ураган-175».

Данные для расчета: длина шатуна L = 110 мм; радиус кривошипа R = 30 мм; вес поршня с деталями и части шатуна G_п = 276 г; вес части шатуна и деталей кривошипного подшипника G_к = 118 г. Общий вес шатуна G_ш = 134 г.

n = 10000 об/мин; ω = 1047,2 Г/сек; ω²= 1096627,84 1°/сек.

Вес соответствующих частей шатуна получен путем поочередного взвешивания каждой головки относительно оси противоположной головки; при этом линия, соединяющая их оси, должна быть строго горизонтальна (G_шп + G_шк = G_ш; соответственно: 55 + 79 = 134 г).

Определим необходимую точность уравновешивания деталей, участвующих во вращательном движении. Возьмем вес 1 г; тогда:


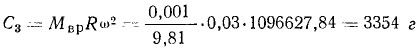
Из этого следует, что ошибка в уравновешивании на 1 г при 10000 об/мин создает инерционные силы первого порядка, равные 3 кг 354 г.

Все это остается справедливым и для деталей, движущихся прямолинейно, т. е. для поршня с его деталями и верхней части шатуна, так как C₁ = M_пRω². Смещение 1 г противовеса по радиусу кривошипа на ±1 дает:


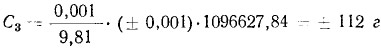
Для уравновешивания двигателя нам необходимо установить противовесы, приведенные к радиусу R = 30 мм.

Исходя из конструкции коленчатого вала ГПМ «Ураган-175» (или «Дельфин») мы вынуждены установку противовесов заменить снятием (выбиранием) металла из щек коленчатого вала. Определим количество удаленного металла: С_п = 276 г, так как из вышесказанного следует, что уравновешивать следует только половину, т. е. 138 г. G_к = 118 г (этот вес должен быть уравновешен полностью). Общий вес снимаемого металла составляет:


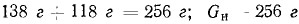
т. е. по 128 г на каждую щеку коленчатого вала (G_н/2 = 128 г). Но на каждой щеке уже сделаны выборки для размещения головки шатуна и смазки подшипника. Пользуясь соответствующими уравнениями стереометрии, следует определить объем и центр тяжести этой выборки. Определив объем, определяем вес: P=γυ, где υ = 9,11 см³ (объем выборки для «Урагана-175»), а γ = 7,85 г/см³ — плотность металла. Отсюда G = 7,85 · 9,11 = 71,51 г. Центр тяжести лежит на радиусе R' = 31,13 мм.

Приведем вес выборки к радиусу кривошипа R = 30 мм:


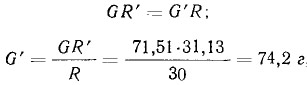
где R'—радиус центра тяжести.

Остаток неуравновешенности:


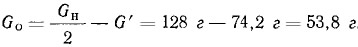
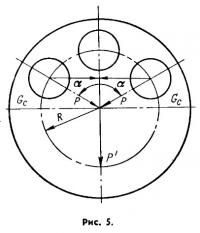
Остаток целесообразно выбрать двумя сверлениями, расположенными симметрично относительно радиуса кривошипа (рис. 5). Для простоты решения сверления выполним на радиусе R = 30 мм. Определим вес каждого сверления (высверленного металла): G₀ = 2G_Ccosα. Угол возьмем а=60°, тогда:


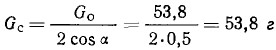
так как эти отверстия для уменьшения потерь необходимо закрыть заглушками, вес высверливаемого металла следует увеличить на вес заглушек.

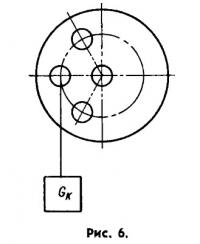
Качество уравновешивания зависит от точности выполнения расчетов и обработки коленчатого вала. Проверка уравновешенности производится на призмах для статической балансировки. Проверку следует производить для каждой щеки раздельно, т. е. при разобранном коленчатом вале; при этом заглушки, учтя их вес в грузе для проверки, запрессовывать не следует. Расположение половины коленчатого вала на призмах и крепления контрольного груза ясно из рис. 6.

Контрольный вес равен:


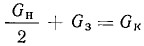
где G_н — полный неуравновешенный вес;
G_з — вес заглушек;
G_к — контрольный вес.

Вместо пальца кривошипа следует вставить пробку из того же материала, что и палец. Посадка заглушки ходовая. Строго из центра пробки должен выходить тонкий штырь для подвески груза.

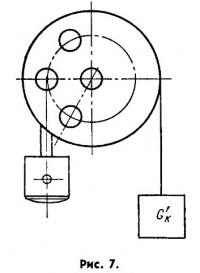
Проверка коленчатого вала в сборе с шатуном и поршнем производится как показано на рис. 7.

Контрольный вес для коленчатого вала в сборе определяется следующим образом:


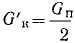
т. е. контрольный вес равен половине веса всех частей, движущихся возвратно-поступательно. Этот вес должен быть приложен на противоположном конце продолжения радиуса кривошипа; так как приложение его на радиусе, равном радиусу кривошипа, может представить некоторую сложность, то его можно пересчитать на любой другой более удобный радиус:


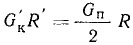
где R' — новый выбранный радиус;
R — радиус кривошипа.
Для приведенного примера:


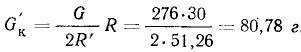
Вывод. Одноцилиндровый двигатель ГПМ типа «Ураган-175», «Дельфин» (RM-175) может быть уравновешен в наилучшем случае только на половину веса деталей, Движущихся возвратно-поступательно, но и такой степени уравновешенности при помощи статической балансировки достигнуть удается не всегда.

Наиболее высокие результаты уравновешивания можно получить при динамической балансировке на специальном балансировочном станке.