С такого простейшего определения начинается наука о корабле, именуемая «теорией корабля», (а точнее — ее раздел, называемый статикой корабля). Оно и понятно. Ведь если построенный корабль не будет обладать плавучестью, т. е. вместо того, чтобы плавать, пойдет ко дну, ни о каких других важнейших его качествах (например, остойчивости или ходкости) просто не придется вести речь.
Для начала рассмотрим два упомянутых Крыловым основополагающих понятия: «плавучесть» и «заданная осадка», а точнее, их взаимосвязь1.
Считается, что человек научился перемещаться по воде на специально создаваемых для этой цели плавучих средствах около сорока тысяч лет назад. Конечно, и в доисторические времена всякий из «владельцев» этих плавсредств по опыту более или менее точно представлял, какое количество груза может принять его «судно», чтобы оставаться на плаву и совершать более или менее безопасные плавания, но ни о какой «заданной», т. е. заранее, до постройки судна, установленной расчетом осадке не могло быть н речи. Слепо использовался передаваемый из поколения в поколение опыт, накопленный дорогой ценой. Не было ни обобщения этого опыта, ни какого-либо представления о физических основах плавания тел.
Лишь за 230 лет до нашей эры были открыты основные законы плавучести. Сделал это великий физик и математик древности — Архимед — грек, живший в Сиракузах на острове Сицилия. Каждому со школьных лет «известно , что он открыл свой закон, сидя в ванне, после чего с криком «эврика!» выскочил на улицу. На самом деле это не более чем исторический анекдот, дошедший до нас благодаря Плутарху — автору «Сравнительных жизнеописаний выдающихся греков и римлян».
Сочинение Архимеда под названием «О плавающих телах» состоит из двух книг. Путем логических рассуждений он всесторонне рассматривает почти все вопросы, относящиеся к плавучести судна и даже к основам остойчивости.
Основные его «предположения», содержащие формулировки закона плавучести, таковы:
«VI. Тела, более легкие, чем жидкость, опущенные в эту жидкость насильственно, будут выталкиваться вверх с силой, равной тому весу, на который жидкость, имеющая равный объем с телом, будет тяжелее этого тела».
«VII. Тела, более тяжелые, чем жидкость, опущенные в эту жидкость, будут погружаться, пока не дойдут до самого низа, и в жидкости станут легче на величину жидкости в объеме, равном объему погруженного тела».
Практически это означает, что корабль будет погружаться в воду до тех пор, пока его вес не уравняется с весом воды, вытесненной погруженной частью его корпуса. Поэтому вес плавающего судна и называют водоизмещением.
Иными словами, плавучесть судна определяется законом Архимеда, из которого следует, что на плавающее судно действует равнодействующая сила гидростатического давления (сила плавучести или сила поддержания), равная по величине и противоположная по направлению силе тяжести судна. Судно плавает, находясь в состоянии равновесия, поскольку две эти силы уравновешивают друг друга.
Сразу же подчеркнем, что открытые Архимедом законы на протяжении столетий не оказывали никакого влияния на кораблестроение. Оно по-прежнему продолжало оставаться ремеслом, в лучшем случае — искусством.
И уж тем более никакого практического значения не имела работа канонира британского флота Уильяма Буэна, который не только развил «предположения» великого грека, но и сформулировал ни много ни мало, а основы теории подводного плавания. В 1578 г. вышла в свет его небольшая брошюра под многозначительным названием: «Изобретения или устройства, совершенно необходимые для всех генералов и капитанов или командиров людей как на море, так и на земле». В ней написано: «Всякий предмет, который тонет сам собою, тяжелее равного ему объема воды, а если он легче этого объема, то он всплывает и появляется на поверхности согласно соотношению весов; и так как оказалось, что это верно, то всякая находящаяся в воде масса или тело, имеющее всегда тот же самый вес, каков бы ни был его объем, если его можно по желанию увеличить или уменьшить, может, если вы захотите, всплывать или тонуть по вашему выбору». Чем ни намек на всплытие и погружение подводных аппаратов при помощи изменения объема (продувка или заполнение балластных цистерн) либо аварийное всплытие при помощи изменения веса (отдача балласта)?
Голландский инженер и математик Симон Стевин (тот самый, который ввел в Европе десятичные дроби) в своем классическом труде «Принципы равновесия» (1586 г.) не только изящной формулировкой подтвердил закон Архимеда, но и доказал, что для равновесия плавающего тела его центр тяжести должен лежать на одной вертикали с центром величины (точкой приложения равнодействующей сил поддержания, расположенной в центре тяжести объема подводной части судна).
Информация об изображении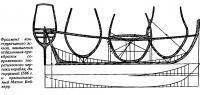
Фрагмент конструктивного эскиза - прообраза современного теоретического чертежа
Почти одновременно со Стевином те же вопросы гидростатики решал гениальный итальянский ученый Галилео Галилей. В его «Рассуждениях о телах, пребывающих в воде, и о тех, которые в ней движутся» (1612 г.) изложен оригинальный подход к обоснованию теории плавания тел; одновременно автор полемизировал с теми, кто считал, что оно определяется прежде всего формой тела, и ставил вопрос о весе жидкости, способной удержать тело заданного веса.

Фрагмент конструктивного эскиза - прообраза современного теоретического чертежа
Перейти от всех этих теоретических формулировок к практике долгое время не позволял общий уровень развития мировой науки и техники. В частности, корабелам предстояло научиться с достаточной точностью представлять сложную форму корпуса графически — в виде так называемого «теоретического чертежа», на котором в трех прямоугольных проекциях (бок, корпус, полуширота) в масштабе изображается пересечение наружной поверхности корпуса тремя системами плоскостей (параллельных диаметральной плоскости, мидедь-шпангоуту и грузовой ватерлинии). Упомянем, что на протяжении многих веков мастера обходились без такого чертежа. Для представления о форме корпуса делалась его масштабная модель. Чаще всего это была модель половины корпуса, разрезанного вдоль по плоскости симметрии — по ДП. С этой модели (у нас ее еще совсем недавно называли «блокмоделью») снимались все размеры, необходимые для вычерчивания основных деталей корпуса в натуральную величину («разбивки»), их изготовления и установки. Не будем забывать: особой точности и не требовалось, поскольку детали вытесывались из дерева и главным инструментом оставался плотницкий топор.
Пока сами суда традиционных типов были довольно просты ми по конструкции и небольшими, потребности в предварительной разработке их детальных чертежей не возникало. Каждый мастер вел (и передавал сыновьям) секретные записи, обобщающие личный опыт, и естественно старался не отходить от испытанного прототипа. Однако суда становились все более сложными и крупными. При постройке их уже нельзя было доверять памяти и интуиции одного человека, а сами записи, пересыпанные цифровыми зависимостями, становились все более громоздкими и запутанными.
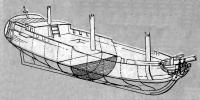
В XVI в. уже появились рисованные или, правильнее сказать, снабженные эскизами наставления по постройке судов. Теперь все чаще с самого начала работ не только внешний вид, но и конструкция будущего судна, и размеры основных деталей его корпуса устанавливались в виде рисунка. Первенствовал в этом англичанин Мэтью Бейкер, сравнительно подробно изобразивший проект корабля на бумаге. В связи с этим ему первому в стране в 1571 г. и было присвоено звание «корабельный мастер». Самые первые проектные чертежи корабля можно видеть в приписываемом Бейкеру манускрипте «Фрагменты старого английского кораблестроения» (ок. 1586 г.).
Тем не менее, подчеркнем, что проект в целом оставался лишь набором не связанных общей теоретической базой изображений, отражающих опыт и художественные способности корабельного мастера.
Сделать корабль сильнее, чем у противника, можно было лишь увеличивая число пушек и, следовательно, размерения. Тормозом на этом пути и стало отсутствие теоретической основы, которая позволяла бы, создавая проект, гарантировать определенный уровень всех качеств, необходимых будущему кораблю
История флотов свидетельствует, что ошибки, неизбежные при проектировании «вслепую» столь сложных плавучих сооружений, как многопушечные трех-дечные корабли, обходились уже слишком дорого Приведем только два примера.
19 июля далекого 1545 г. лучший корабль Британии — 91-пушечная четырехмачтовая каракка «Мэри Роуз», выходя из Портсмута навстречу врагу, перевернулась и затонула. В старой хронике причина гибели записана классически ясно: «Перегруженный артиллерией и воинами в доспехах (на корабле водоизмещением около 1500 т находилось в общей сложности около 700 человек; спаслось не более 40 — О. Б.) утонул во время поворота из-за того, что прорезанные очень низко орудийные порты подветренного борта были открыты».
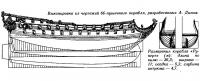
Ныне стал музеем — памятником техники поднятый со дна 64-пушечный «королевский» корабль «Ваза», построенный в Швеции лучшими мастерами, приглашенными из Голландии. В день вступления своего в строй 10 августа 1628 г. этот великолепный, богато украшенный корабль при первом же порыве ветра перевернулся, зачерпнув воду орудийными портами подветренного борта. При судебном разбирательстве выяснилось, что, стараясь любой ценой повысить боевую мощь «Вазы», автор проекта не смог обеспечить остойчивость корабля, перегруженного пушками (весом около 80 т). Он рассчитывал понизить положение его центра тяжести добавлением каменного балласта на днище. Однако сделать это оказалось невозможно, ибо, как показал на суде спасшийся артиллерийский офицер Йенсен, после полной загрузки корабля на плаву «порты нижней батарейной палубы отстояли всего лишь на 3—4 фута от ватерлинии»...
В обоих случаях основная причина трагедии одинакова. Мастер, рисуя корабль, отличающийся от уже построенных, не знал и не мог знать его осадки при полной боевой нагрузке. Прорезанные порты нижней батарейной палубы оказывались расположенными слишком низко — высота надводного борта была недостаточной.
Кораблестроители, каждый по-своему оценивая накопленный опыт «гонки вооружений», стали отказываться от нагромождения многоярусных надстроек, ввели учет веса поступающих на корабль грузов. Порты нижнего ряда прорезали теперь лишь тогда, когда уже была более или менее ясна фактическая осадка.
Вот опять-таки характерный пример. Отец и сын Петты — представители династии корабельных мастеров «владычицы морей» — 13 октября 1637 г. спустили на воду огромный 104-пушечный корабль «Властелин морей». И, посмотрев на его слишком большую осадку, начали переделки. Как пишет Э. Генриот — автор «Краткой истории судостроения» (Л., «Судостроение», 1974), «кормовые надстройки были придирчиво уменьшены, а бак и кормовая полупалуба — укорочены» (исчезла непрерывная верхняя орудийная палуба). Приводимые разными авторами цифры отличаются, но можно сделать вывод, что и после всех переделок «Властелина» его осадка при полном водоизмещении (6,75 м) на целый метр превышала «проектную», установленную, как мы уже знаем, не расчетом, а умозрительно, путем сравнения с меньшими кораблями, ранее построенными теми же Петтами.
Неудивительно, что раньше или позже, но во всех флотах были введены разработанные на чисто статистической основе своеобразные «отраслевые стандарты». В Англии, например, все боевые корабли делились на шесть рангов В зависимости от полагающегося числа пушек для корабля каждого ранга жестко оговаривались тоннаж, основные размерения, а зачастую и минимальные размеры основных детален корпуса и рангоута
Итак, для решения назревших проблем практики требовалось, во-первых, научиться строить точные чертежи обводов корабля и, во-вторых, разработать какие-то достаточно простые способы расчета по теоретическому чертежу площадей и объемов, ограниченных криволинейными поверхностями корабельного корпуса. В принципе вторая задача могла быть решена при помощи интегрального исчисления, которое возникло еще в античные времена и было основано на аппроксимации — приближенном выражении рассматриваемых объектов сложной формы в виде составленных из большого числа простейших фигур или пространственных тел (прямоугольников, параллелепипедов, цилиндров и т. п.). Можно упомянуть в этой связи, например, работу известного астронома И. Кеплера под глубокомысленным и длинным названием: «Новая стереометрия винных бочек, преимущественно австрийских, как имеющих самую выгодную форму,...» и т. д. и т. п. Здесь (1615 г.) был предложен пригодный для практики метод вычисления объемов с заменой криволинейных линий прямолинейными отрезками.
Другими словами, к середине XVII века ученые (в первую очередь математики Франции), опережая практиков, уже подготовили необходимый математический инструмент.
И первые попытки применения давно известного закона плавучести к практике судостроения при помощи математики уже предпринимались, опять-таки, в первую очередь, во Франции, но были они редкими и робкими.
Первым блистательно решил задачу в полном ее объеме и, говоря словами академика А. Н. Крылова, впервые применил к делу судостроения закон Архимеда англичанин — 28-летний «корабельный мастер» Антони Дин2. Произошло это в портовом городе Харидже в 1666 г. при постройке 66-пушечного корабля «Руперт».
Предоставим слово современнику и другу этого корабела Самуэлю Пепису — аристократу, сёрваеру по снабжению флота, а в дальнейшем — секретарю Адмиралтейства и президенту Лондонского королевского общества. В его дневнике, отнюдь не предназначенном для постороннего глаза, 18—19 мая 1666 г. записано: «Господин Дин и я говорили о его корабле «Руперт», постройка которого была столь успешна, что это делает ему честь, а я горжусь тем, что рекомендовал его. Король, герцог и все говорят, что это лучший из всех когда-либо построенных кораблей. Дин объяснил мне свой способ определения осадки корабля расчетом прежде его постройки, что является секретом и привело в восторг короля и всю свиту. Он первый кораблестроитель, который мог предсказать углубление корабля до спуска его на воду». И сразу же добавим: Дин был настолько уверен в своем «предсказании», что прорезал порты нижнего ряда еще на стапеле и даже якобы при гласил на церемонию спуска на воду этого ничем другим не примечательного корабля 3-г о ранга самого короля. Осадка благополучно спущенного на воду «Руперта» точно соответствовала заранее указанной Дином и это естественно стало сенсацией в узком кругу английских корабелов.
Вернемся теперь к дневнику Пеписа. Слово «секрет» было употреблено им в самом прямом значении. Серьезное совершенствование процесса проектирования и постройки корабля, поднимающее самый уровень развития этой отрасли техники (ведущей — по тем временам), не могло не считаться секретным. Надо иметь в виду многолетнее соперничество великих морских держав и поэтому ревнивое внимание к успехам соседей в кораблестроении. С одной стороны, тот же Антони Дин с молодых лет интересовался работами французов в области применения математики. А с другой, девять лет спустя после «Руперта», был гостем французских корабелов и, очевидно, в какой-то форме удовлетворил их любопытство, поделившись своим драгоценным опытом. За что и угодил в Тауэр, обвиненный в сугубо нежелательных связях с Францией...
К 1675 г. Дин успел построить «по-новому» 12 кораблей, и все они, начиная от небольшой яхты «Кливленд» (вооруженной) и кончая огромным кораблем 1-го ранга «Джеймс Ройял», неизменно заслуживали самую высокую оценку. Дин занимал все более высокие должности. Сын простого моряка — он был удостоен рыцарского звания и стал именоваться сэром Антони. Милость короля Карла II к своему любимцу простиралась так далеко, что он командировал Дина (и Пеписа) во Францию с заданием построить там для версальского двора две «непревзойденные яхты». От того, что получилось, Людовик XIV пришел в восторг и подарил Дину свой портрет, обрамленный бриллиантами Однако стоило отношениям между Англией и Францией испортиться, и оба — Дин и Пепис (к тому времени ставшие членами парламента) по ложному доносу были арестованы и препровождены в знаменитую лондонскую крепость-тюрьму.
Только через десять месяцев после неоднократных разбирательств оба вышли на свободу и еще через год были наконец восстановлены в правах В 1681 г. Дина избрали членом Королевского общества, затем он стал Инспектором кораблестроения и написал несколько книг. В частности, в 1670 г. в Кембридже вышла в свет его известная работа «Доктрина корабельной архитектуры». Одна из книг Дина еще при его жизни была переведена на русский и издана в Петербурге (1711 г ) под названием «Размеры корабля с измерениями для описания или черчения кораблестроительного корпуса».
Отметим, что Петр I, будучи в Англии в 1698 г., не просто встречался с сэром Антони3, но и пользовался многими его советами и указаниями. А сына его Джона уговорил поехать в Россию, чтобы строить в Воронеже корабли для Русского флота.
Попробуем теперь разобраться в том, чем же именно так удивил современников сэр Антони.
Мы уже знаем, что для предвычисления осадки он использовал основное уравнение плавучести, которое в классических учебниках теории корабля получило вид
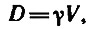
где γ — удельный вес (плотность) воды, D — весовое водоизмещение или вес корабля (в тоннах), V — объемное водоизмещение или объем погруженной (подводной) части корабля (в м3) при осадке, соответствующей D.
Можно для упрощения считать удельный вес воды равным единице. Итак, уравнение плавучести примет вид D≈V. Пока судно находится на плаву, любому изменению D соответствует такое же по величине изменение погруженного объема V. Соответственно изменяется и осадка судна Т: если D и V возрастают, она увеличивается, если D и V уменьшаются — судно подвсплывает и Т становится меньше. Задача Дина и состояла в том, чтобы для конкретного корабля заранее связать величины D=V и значение осадки Т.
Во время постройки «Руперта» на верфи велся, как принято сейчас говорить, «весовой журнал». Взвешивались все без исключения детали, идущие на стапель, регистрировались поступающие на корабль грузы. То, что не могло быть взвешено на момент подведения итогов, очевидно оценивалось по результатам взвешивания при постройке других кораблей. Просуммировав составляющие нагрузки, Дин получил D — весовое водоизмещение корабля «Руперт», хотя он еще стоял на стапеле. Та же самая цифра, но в соответствующих единицах уже не веса, а объема обозначала значение V — объема подводной части корпуса «Руперта», когда он будет находиться на плаву.
Едва ли не главная заслуга Дина заключалась в том, что он, будучи, кстати сказать, прекрасным чертежником и рисовальщиком, сделал чертеж корпуса корабля из поначалу чисто «демонстрационного», а затем все чаще приспособляемого для решения каких-то технологических вопросов, действительно «теоретическим» — пригодным для решения целого круга задач, в конце концов и составивших современную теорию корабля. Он усовершенствовал саму технику построения теоретического чертежа — в первую очередь проекции «корпус» и даже составил специальную инструкцию по ее вычерчиванию. Можно сказать, что «корпус» того же корабля «Руперт» отличается от «корпуса» современных нам теоретических чертежей в основном лишь тем, что отсутствуют «батоксы» — сечения вертикальными плоскостями, параллельными ДП. Вместо них строились диагональные сечения — «рыбины» для согласования сложных обводов в районе скулы.
Итак, сэр Антони имел на проекции «корпус» точные очертания шпангоутов4 и знал расстояние между ними — «шпацию». Это давало возможность представить корпус корабля как бы разрезанным поперечными сечениями (шпангоутами) на отсеки-ломтики, «толщина» которых равна шпации, и вычислять объем корпуса как простую сумму их объемов.
А что такое объем тела, ограниченного параллельными плоскостями? Ясно, что это средняя площадь обоих шпангоутов, умноженная на «толщину» (т е. на шпацию) Таким образом для расчета объемного водоизмещения V было необходимо рассчитать расположенные ниже КВЛ площади каждого теоретического шпангоута и просуммировать объемы всех отсеков.
Сейчас такие операции, как расчет площадей шпангоутов (т. е. площадей, ограниченных кривыми), не просто механизированы применением планиметров, но и полностью автоматизированы благодаря широкому использованию ЭВМ. А во времена сэра Антони (как, впрочем, и теперь при любительских расчетах) решение даже простейших задач статики корабля занимало очень много времени. (Представление о том, как это делалось вплоть до недавнего времени, дает пример расчета площади шпангоута в табличной форме по приближенному методу трапеций).
Мы можем попытаться условно воспроизвести дальнейший ход работы Дина по предвычислению осадки корабля 3-го ранга «Руперт» По теоретическому чертежу он рассчитал объемное водоизмещение будущего корабля V1 при погружении его по какую-то условную КВЛ1, которая соответствует средней осадке кораблей этого ранга Т1=4,8 м. Допустим (цифры условные), что получилось V1=980 м3. Однако со времен Архимеда известно, что V всегда должно быть равно D. Сравниваем V1 с уже известным нам значением D, которое установлено фактическим взвешиванием (допустим, оно было равно 1200 т).
Налицо явное нарушение равенства, так как 980<1200 Это говорит о том, что при данном весе корабля объем его погруженной части будет больше. Иными словами, и его осадка будет не 4,8 м, а несколько больше. Весь расчет должен быть повторен для какого-то нового положения КВЛ Допустим, что при осадке Т2=5,4 м мы получили V2=1350 т. И на этот раз равенство нарушено, но теперь придется сделать обратный вывод: следует уменьшить значение осадки...
Работа продолжается до тех пор, пока числовые значения Vn и D не совпадут. То положение КВЛ, при котором Vn=1200 м3, и будет соответствовать осадке корабля. Пусть в нашем условном примере получится Т=5,2 м; именно такой и была фактическая осадка корабля Руперт», вычисленная Дином. Зная эту величину, он соответственно назначил высоту нижней батарейной палубы и мог заранее прорезать порты, будучи твердо уверенным, что они не окажутся ближе к поверхности воды, чем он считает необходимым.
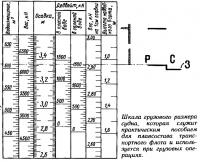
В заключение можно сказать, что от сэра Антони ведут начало современные методы построения строевой по шпангоутам и расчетного определения положения центра величины, построения кривых зависимости объемного и весового водоизмещения судна от осадки. Кривая весового водоизмещения широко применяется в виде так называемой кривой грузового размера. Это простейшая номограмма, по которой очень легко и быстро можно определить новую осадку, получающуюся после приема или снятия груза известного веса, или же наоборот — определить вес груза, который надлежит снять (или принять) для получения заданной осадки.
Для практических целей судоходства кривую грузового размера очень часто представляют в виде более удобной шкалы грузового размера. На ней кроме осадки и весового водоизмещения принято показывать остающуюся высоту надводного борта и грузоподъемность (дедвейт) судна, а также число тонн, вызывающих изменение осадки судна на 1 см/
Примечания
1. В какой-то мере, с точки зрения моряка, эти вопросы уже затрагивались в статье Л. Скрягина «Корабли, грузовая марка и тонны», напечатанной в предыдущем номере. Там говорилось, главным образом, о нормировании предельной осадки эксплуатируемого судна как способе контроля за сохранением безопасной высоты надводного борта (запаса плавучести).
2. Подробнее о нем рассказывается в статье А. Н. Холодилнна «Кораблестроитель, удививший современников» (в сб. «Человек, море, техника — 88», Л., «Судостроение», 1988)
3. До того Петр I изучал корабельное дело в Голландии. Его основной учитель — одни из лучших голландских корабельных мастеров Герит Клас Поль, закончив обучение. выдал ученику патент, в котором перечислил все, чему тот успел научиться. Особо отмечено, что «корабельную архитектуру и черчение планов его благородие изучил основательно и уразумел эти предметы в такой степени, сколько мы сами их разумеем». Тем не менее Петр остался недоволен обучением («зело стало противно») Он был разочарован именно тем, что голландские мастера «строят суда просто по навыку и опыту, без всяких хитростных чертежей».
В Англии Петр пробыл три с половиной месяца, работал на королевской верфи в Дептфорде, изучал математику, основы теории корабля и способы построения теоретического чертежа, т. е. именно то, в чем силен был Антони Дин. Впоследствии Петр I признавал, что «навсегда остался бы только плотником, если бы не поучился у англичан».
4. Речь идет о так называемых «теоретических» шпангоутах, которых обычно бывает гораздо меньше, чем конструктивных «практических» шпангоутов в корпусе судна. Как правило, при построении теоретического чертежа длину проектируемого судна по КВЛ делят на небольшое и удобное для вычислений число теоретических шпангоутов (например, 10 или 20). Их очертания и изображают на проекции «корпус». Одинаковое по всей длине судна расстояние между ними называют «теоретической шпацией».